
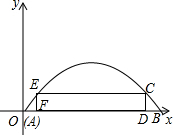
 如图,已知一抛物线形大门,其地面宽度AB=18m,最高高度为8.1m,同学们站在门内想拉一条距离地面高1.7m的宣传条幅CE,其顶端恰好等在抛物线形门上C、E处.
如图,已知一抛物线形大门,其地面宽度AB=18m,最高高度为8.1m,同学们站在门内想拉一条距离地面高1.7m的宣传条幅CE,其顶端恰好等在抛物线形门上C、E处.
|
|
| 1 |
| 30 |
| 6 |
| 5 |
| 1 |
| 30 |
| 6 |
| 5 |
| 373 |
| 373 |
| 373 |
| 373 |
| 373 |
| 373 |


科目:初中数学 来源: 题型:
|
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
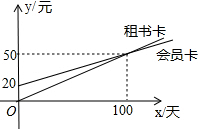 某图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡,使用这两种卡租书,租书金额y(元)与租书时间x(天)之间的关系如图所示:
某图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡,使用这两种卡租书,租书金额y(元)与租书时间x(天)之间的关系如图所示:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com