
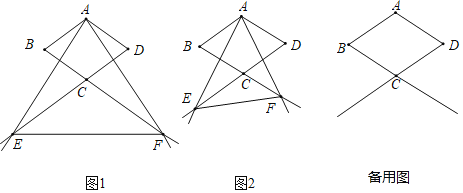
【题目】如图,菱形ABCD中,∠B=60°,AB=3cm,过点A作∠EAF=60°,分别交DC,BC的延长线于点E,F,连接EF.
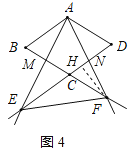
(1)如图1,当CE=CF时,判断△AEF的形状,并说明理由;
(2)若△AEF是直角三角形,求CE,CF的长度;
(3)当CE,CF的长度发生变化时,△CEF的面积是否会发生变化,请说明理由.
【答案】(1) △AEF是等边三角形,证明见解析;(2) CF=![]() ,CE=6或CF=6,CE=
,CE=6或CF=6,CE=![]() ;(3) △CEF的面积不发生变化,理由见解析.
;(3) △CEF的面积不发生变化,理由见解析.
【解析】
(1)证明△BCE≌△DCF(SAS),得出∠BE=DF,CBE=∠CDF,证明△ABE≌△ADF(SAS),得出AE=AF,即可得出结论;
(2)分两种情况:①∠AFE=90°时,连接AC、MN,证明△MAC≌△NAD(ASA),得出AM=AN,CM=DN,证出△AMN是等边三角形,得出AM=MN=AN,设AM=AN=MN=m,DN=CM=b,BM=CN=a,证明△CFN∽△DAN,得出![]() ,得出FN=
,得出FN=![]() ,AF=m+
,AF=m+![]() ,同理AE=m+
,同理AE=m+![]() ,在Rt△AEF中,由直角三角形的性质得出AE=2AF,得出m+
,在Rt△AEF中,由直角三角形的性质得出AE=2AF,得出m+![]() =2(m+
=2(m+![]() ),得出b=2a,因此
),得出b=2a,因此![]() ,得出CF=
,得出CF=![]() AD=
AD=![]() ,同理CE=2AB=6;
,同理CE=2AB=6;
②∠AEF=90°时,同①得出CE=![]() AD=
AD=![]() ,CF=2AB=6;
,CF=2AB=6;
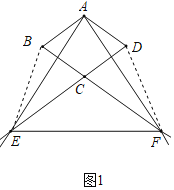
(3)作FH⊥CD于H,如图4所示:由(2)得BM=CN=a,CM=DN=b,证明△ADN∽△FCN,得出![]() ,由平行线得出∠FCH=∠B=60°,△CEM∽△BAM,得出
,由平行线得出∠FCH=∠B=60°,△CEM∽△BAM,得出![]() ,得出
,得出![]() ,求出CF×CE=AD×AB=3×3=9,由三角函数得出CH=CF×sin∠FCH=CF×sin60°=
,求出CF×CE=AD×AB=3×3=9,由三角函数得出CH=CF×sin∠FCH=CF×sin60°=![]() CF,即可得出结论.
CF,即可得出结论.
解:(1)△AEF是等边三角形,理由如下:
连接BE、DF,如图1所示:
∵四边形ABCD是菱形,
∴AB=BC=DC=AD,∠ABC=∠ADC,
在△BCE和△DCF中,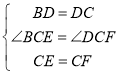 ,
,
∴△BCE≌△DCF(SAS),
∴∠BE=DF,CBE=∠CDF,
∴∠ABC+∠CBE=∠ADC+∠CDF,
即∠ABE=∠ADF,
在△ABE和△ADF中,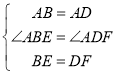 ,
,
∴△ABE≌△ADF(SAS),
∴AE=AF,又∵∠EAF=60°,
∴△AEF是等边三角形;
(2)分两种情况:
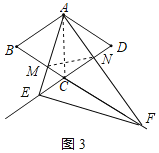
①∠AFE=90°时,连接AC、MN,如图2所示:
∵四边形ABCD是菱形,
∴AB=BC=DC=AD=3,∠D=∠B=60°,AD∥BC,AB∥CD,
∴△ABC和△ADC是等边三角形,
∴AC=AD,∠ACM=∠D=∠CAD=60°=∠EAF,
∴∠MAC=∠NAD,
在△MAC和△NAD中,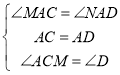 ,
,
∴△MAC≌△NAD(ASA),
∴AM=AN,CM=DN,
∵∠EAF=60°,
∴△AMN是等边三角形,
∴AM=MN=AN,
设AM=AN=MN=m,DN=CM=b,BM=CN=a,
∵CF∥AD,
∴△CFN∽△DAN,
∴![]() ,
,
∴FN=![]() ,
,
∴AF=m+![]() ,
,
同理:AE=m+![]() ,
,
在Rt△AEF中,∵∠EAF=60°,
∴∠AEF=30°,
∴AE=2AF,
∴m+![]() =2(m+
=2(m+![]() ),
),
整理得:b2﹣ab﹣2a2=0,
(b﹣2a)(b+a)=0,
∵b+a≠0,
∴b﹣2a=0,
∴b=2a,
∴![]() =
=![]() ,
,
∴CF=![]() AD=
AD=![]() ,
,
同理:CE=2AB=6;
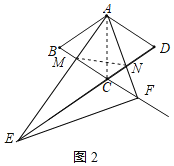
②∠AEF=90°时,连接AC、MN,如图3所示:
同①得:CE=![]() AD=
AD=![]() ,CF=2AB=6;
,CF=2AB=6;
(3)当CE,CF的长度发生变化时,△CEF的面积不发生变化;理由如下:
作FH⊥CD于H,如图4所示:
由(2)得:BM=CN=a,CM=DN=b,
∵AD∥CF,
∴△ADN∽△FCN,
∴![]() ,
,
∵CE∥AB,
∴∠FCH=∠B=60°,△CEM∽△BAM,
∴![]() ,
,
∴![]() ,
,
∴CF×CE=AD×AB=3×3=9,
∵CH=CF×sin∠FCH=CF×sin60°=![]() CF,
CF,
△CEF的面积=![]() CE×FH=
CE×FH=![]() CE×
CE×![]() CF=
CF=![]() ×9×
×9×![]() =
=![]() ,∴△CEF的面积是定值,不发生变化.
,∴△CEF的面积是定值,不发生变化.


科目:初中数学 来源: 题型:
【题目】定义:如果三角形的两个内角![]() 与
与![]() 满足
满足![]() ,那么称这样的三角形为“类直角三角形”.
,那么称这样的三角形为“类直角三角形”.
尝试运用
(1)如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的平分线.
的平分线.
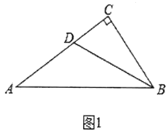
①证明![]() 是“类直角三角形”;
是“类直角三角形”;
②试问在边![]() 上是否存在点
上是否存在点![]() (异于点
(异于点![]() ),使得
),使得![]() 也是“类直角三角形”?若存在,请求出
也是“类直角三角形”?若存在,请求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
类比拓展
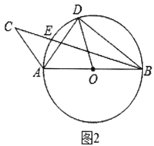
(2)如图2,![]() 内接于
内接于![]() ,直径
,直径![]() ,弦
,弦![]() ,点
,点![]() 是弧
是弧![]() 上一动点(包括端点
上一动点(包括端点![]() ,
,![]() ),延长
),延长![]() 至点
至点![]() ,连结
,连结![]() ,且
,且![]() ,当
,当![]() 是“类直角三角形”时,求
是“类直角三角形”时,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学兴趣小组研究某型号冷柜温度的变化情况,发现该冷柜的工作过程是:当温度达到设定温度![]() 时,制冷停止,此后冷柜中的温度开始逐渐上升,当上升到
时,制冷停止,此后冷柜中的温度开始逐渐上升,当上升到![]() 时,制冷开始,温度开始逐渐下降,当冷柜自动制冷至
时,制冷开始,温度开始逐渐下降,当冷柜自动制冷至![]() 时,制冷再次停止,……,按照以上方式循环进行.
时,制冷再次停止,……,按照以上方式循环进行.
同学们记录了44![]() 内15个时间点冷柜中的温度
内15个时间点冷柜中的温度![]() 随时间
随时间![]() 的变化情况,制成下表:
的变化情况,制成下表:
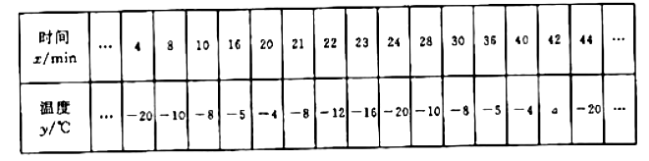
(1)通过分析发现,冷柜中的温度![]() 是时间
是时间![]() 的函数.
的函数.
①当![]() 时,写出一个符合表中数据的函数解析式 ;
时,写出一个符合表中数据的函数解析式 ;
②当![]() 时,写出一个符合表中数据的函数解析式 ;
时,写出一个符合表中数据的函数解析式 ;
(2)![]() 的值为 ;
的值为 ;
(3)如图,在直角坐标系中,已描出了上表中部分数据对应的点,请描出剩余对应的点,并画出![]() 时温度
时温度![]() 随时间
随时间![]() 变化的函数图象.
变化的函数图象.

查看答案和解析>>
科目:初中数学 来源: 题型:
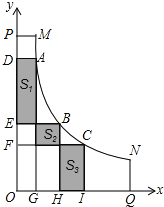
【题目】六一儿童节,小文到公园游玩.看到公园的一段人行弯道MN(不计宽度),如图,它与两面互相垂直的围墙OP、OQ之间有一块空地MPOQN(MP⊥OP,NQ⊥OQ),他发现弯道MN上任一点到两边围墙的垂线段与围墙所围成的矩形的面积都相等,比如:A、B、C是弯道MN上的三点,矩形ADOG、矩形BEOH、矩形CFOI的面积相等.爱好数学的他建立了平面直角坐标系(如图),图中三块阴影部分的面积分别记为S1、S2、S3,并测得S2=6(单位:平方米).OG=GH=HI.
(1)求S1和S3的值;
(2)设T(x,y)是弯道MN上的任一点,写出y关于x的函数关系式;
(3)公园准备对区域MPOQN内部进行绿化改造,在横坐标、纵坐标都是偶数的点处种植花木(区域边界上的点除外),已知MP=2米,NQ=3米.问一共能种植多少棵花木?
查看答案和解析>>
科目:初中数学 来源: 题型:
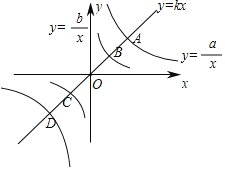
【题目】函数y=kx,y=![]() ,y=
,y=![]() 的图象如图所示,下列判断正确的有_____.(填序号)①k,a,b都是正数;②函数y=
的图象如图所示,下列判断正确的有_____.(填序号)①k,a,b都是正数;②函数y=![]() 与y=
与y=![]() 的图象会出现四个交点;③A,D两点关于原点对称;④若B是OA的中点,则a=4b.
的图象会出现四个交点;③A,D两点关于原点对称;④若B是OA的中点,则a=4b.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,BC=2,O为对角线AC的中点,点P、Q分别从A和B两点同时出发,在边AB和BC上匀速运动,并且同时到达终点B、C,连接PO、QO并延长分别与CD、DA交于点M、N.在整个运动过程中,图中阴影部分面积的大小变化情况是( )

A. 一直增大 B. 一直减小 C. 先减小后增大 D. 先增大后减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个直角三角形纸片![]() 放置在平面直角坐标系中,已知点
放置在平面直角坐标系中,已知点![]() ,点
,点![]() ,点
,点![]() .
.![]() 是边
是边![]() 上的一动点(点
上的一动点(点![]() 不与点
不与点![]() 、
、![]() 重合),沿着
重合),沿着![]() 折叠该纸片,得点
折叠该纸片,得点![]() 的对应点
的对应点![]() .
.
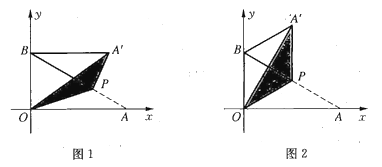
(1)如图1,当点![]() 在第一象限,且满足
在第一象限,且满足![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(2)如图2,当![]() 为
为![]() 中点时,求
中点时,求![]() 的长;
的长;
(3)当![]() 时,直接写出点
时,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
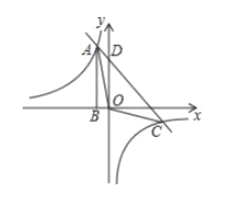
【题目】如图,点![]() 是反比例函数
是反比例函数![]() 图象上的一点,过点
图象上的一点,过点![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() ,
,![]() 的面积为2.点
的面积为2.点![]() 的坐标为
的坐标为![]() .若一次函数
.若一次函数![]() 的图象经过点
的图象经过点![]() ,交双曲线的另一支于点
,交双曲线的另一支于点![]() ,交
,交![]() 轴点
轴点![]() .
.
(1)求反比例函数和一次函数的解析式;
(2)若![]() 为
为![]() 轴上的一个动点,且
轴上的一个动点,且![]() 的面积为5,请求出点
的面积为5,请求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
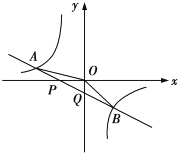
【题目】如图,已知直线![]() 与x轴、y轴相交于P、Q两点,与
与x轴、y轴相交于P、Q两点,与![]() 的图象相交于
的图象相交于![]() 两点,连接OA,OB,给出下列结论:①
两点,连接OA,OB,给出下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④不等式
;④不等式![]() 的解集是
的解集是![]() 或
或![]() ,其中正确的是( )
,其中正确的是( )
A.②③B.③④C.①②③④D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com