
���� ��1������ԭ����ʱ��-�ֹ���ʱ��=4��һ������ϵ�г���ʽ������⼴�ɣ�
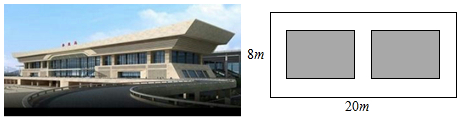
��2�����ݾ��ε������Ϊ56ƽ�����г�һԪ���η�����⼴�ɣ�
��� �⣺��1��������̻�����ԭ�ƻ�ÿ�����x��2��
��������ã�$\frac{46000-22000}{x}$-$\frac{46000-22000}{1.5x}$=4
��ã�x=2000��
�����飬x=2000��ԭ���̵Ľ⣬
�𣺸��̻���Ŀԭ�ƻ�ÿ�����2000ƽ���ף�
��2�������е��Ŀ���Ϊa�ף���������ã�
��20-3a����8-2a��=56
��ã�a=2��a=$\frac{26}{3}$���������⣬��ȥ����
�����е��Ŀ�Ϊ2�ף�
���� ���⿼���˷�ʽ���̼�һԪ���η��̵�Ӧ�ã�����Ĺؼ����ܹ��ҵ�������ϵ���г����̣����ʽ����ʱһ��Ҫ���飮


 ȫ�ſ��䵥Ԫ�����������ܸ�ϰϵ�д�
ȫ�ſ��䵥Ԫ�����������ܸ�ϰϵ�д� Ʒѧ˫�ž�ϵ�д�
Ʒѧ˫�ž�ϵ�д� Сѧ��ĩ���100��ϵ�д�
Сѧ��ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | -4 | D�� | -2.5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ʵ���������ˣ� | 101 | 96 | 113 | 100 | 111 | 108 | 116 | 118 | 97 | 110 |
| ����������ˣ� | -7 | -12 | 5 | -8 | 3 | 0 | 8 | -10 | -11 | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
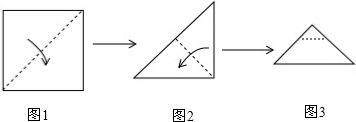
| A�� | 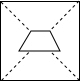 | B�� | 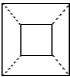 | C�� | 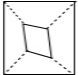 | D�� | 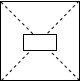 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �� | B�� | �� | C�� | �� | D�� | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
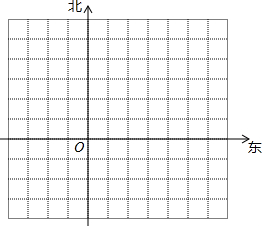 Сǿ��ѧ����������300�ף�������·200�ף������A����һ���飬Ȼ����������500�ף�����������100�ף�����͵�B������ʳ������������400�ף���������800�ף��ص�����C����ͼ����ѧУΪԭ�㽨������ϵ��ͼ�е�ÿ����λ���ȱ�ʾ100�ף�
Сǿ��ѧ����������300�ף�������·200�ף������A����һ���飬Ȼ����������500�ף�����������100�ף�����͵�B������ʳ������������400�ף���������800�ף��ص�����C����ͼ����ѧУΪԭ�㽨������ϵ��ͼ�е�ÿ����λ���ȱ�ʾ100�ף��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com