
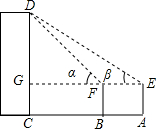
 某数学小组用高为1.2米的仪器测量一教学楼的高CD,如图,距CD一定距离的A处,用仪器测得教学楼顶部D的仰角为β,再在A与C之间选一点B,由B处测出教学楼顶部D的仰角为α,测得A、B之间的距离为4米,若tanα=1.6,tanβ=1.2,则他们能求出教学楼的高吗?
某数学小组用高为1.2米的仪器测量一教学楼的高CD,如图,距CD一定距离的A处,用仪器测得教学楼顶部D的仰角为β,再在A与C之间选一点B,由B处测出教学楼顶部D的仰角为α,测得A、B之间的距离为4米,若tanα=1.6,tanβ=1.2,则他们能求出教学楼的高吗? 分析 设DG=x米,利用正切的定义分别用x表示出FG、EG,根据题意求出x,结合图形计算即可.
解答 解:设DG=x米,
tanα=$\frac{DG}{FG}$,
FG=$\frac{DG}{tanα}$=$\frac{5}{8}$x,
tanβ=$\frac{DG}{GE}$,
GE=$\frac{DG}{tanβ}$=$\frac{5}{6}$x,
由题意得,GE-GF=4,即$\frac{5}{6}$x-$\frac{5}{8}$x=4,
解得x=19.2,
则DC=DG+GC=19.2+1.2=20.4(米).
答:教学楼的高为20.4米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,正切理解仰角俯角分概念、熟记锐角三角函数的定义是解题的关键.


科目:初中数学 来源: 题型:选择题
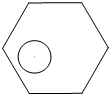 半径为r的圆形纸片在边长为a(a≥$\frac{2}{3}$$\sqrt{3}$r)的正六边形内部任意移动,则在正六边形内部这个圆形纸片“不能接触到的面积”是( )
半径为r的圆形纸片在边长为a(a≥$\frac{2}{3}$$\sqrt{3}$r)的正六边形内部任意移动,则在正六边形内部这个圆形纸片“不能接触到的面积”是( )| A. | a2(2$\sqrt{3}$-aπ) | B. | r2(2π-$\sqrt{3}$) | C. | a2r2(2$\sqrt{3}$-π) | D. | r2(2$\sqrt{3}$-π) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
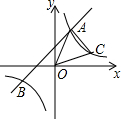 如图,一次函数y=x+2的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,且点A的坐标
如图,一次函数y=x+2的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,且点A的坐标查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲、乙成绩一样稳定 | B. | 甲成绩更稳定 | ||
| C. | 乙成绩更稳定 | D. | 不能确定谁的成绩更稳定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
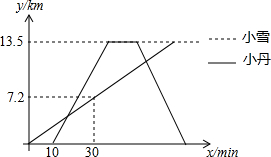 小雪和小丹由甲地到丙地春游,小雪骑自行车从甲地出发骑行至目的地丙地,小雪出发10分钟后,小丹开车从甲地出发,沿小雪行进路线前往丙地,在丙地10分钟后接到电话后按原路返回甲地,小雪和小丹的速度均保持不变,并且小丹速度是小雪速度的2.5倍,如图表示小雪和小丹离甲地的路程y(km)与小雪离开甲地时间x(min)的函数关系图象,小丹在返程途中与小雪再次相遇时的地点距离甲地$\frac{78}{7}$km.
小雪和小丹由甲地到丙地春游,小雪骑自行车从甲地出发骑行至目的地丙地,小雪出发10分钟后,小丹开车从甲地出发,沿小雪行进路线前往丙地,在丙地10分钟后接到电话后按原路返回甲地,小雪和小丹的速度均保持不变,并且小丹速度是小雪速度的2.5倍,如图表示小雪和小丹离甲地的路程y(km)与小雪离开甲地时间x(min)的函数关系图象,小丹在返程途中与小雪再次相遇时的地点距离甲地$\frac{78}{7}$km.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(2,3),双曲线y=$\frac{k}{x}$(x>0)的图象经过BC上的点D与AB交于点E,连接DE,若E是AB的中点.
如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(2,3),双曲线y=$\frac{k}{x}$(x>0)的图象经过BC上的点D与AB交于点E,连接DE,若E是AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com