练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    某商店以16元/支的价格进了一批钢笔，如果以20元/支的价格售出，每月可以卖出200支，而每上涨1元就少卖10支，现在商店店主希望该笔月销售利润达1350元，则每支钢笔应该上涨多少元钱？请你就该种钢笔的涨价幅度和进货量，通过计算给店主提出一些合理建议.

    每支钢笔应该上涨5元或11元钱，月销售利润达1350元；给店主提的建议为：店主对该种钢笔上涨8元，每月进120支钢笔．

    解析试题分析：设上涨元，根据利润=销售量×（定价﹣进价），列出表达式，令=1350，解得每支钢笔应该上涨多少元钱，最后将实际问题转化为求函数最值问题，从而求得最大利润．
    试题解析：设每支钢笔应该上涨元钱，则，解得：，，∴每支钢笔应该上涨5元或11元钱，月销售利润达1350元；∵设利润是元则，∴当时，有最大值为1440；∴给店主提的建议为：店主对该种钢笔上涨8元，每月进120支钢笔．
    考点：1．二次函数的应用；2．应用题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    二次函数y=x2+bx+c的图象经过点（4,3）,（3,0）．
    （1）b=        ,c=         ；
    （2）选取适当的数据填写下表,并在右图的直角坐标系中画出该函数的图像；

    x
    		…
    		 
    		 
    		 
    		 
    		 
    		…
    y
    		…
    		 
    		 
    		 
    		 
    		 
    		…
     
    （3）若将此图象沿x轴向左平移3个单位,直接写出平移后图象所对应的函数关系式           .

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    有两个直角三角形，在△ABC中，∠ACB=90°，AC=3，BC=6，在△DEF中，∠FDE=90°，DE=DF=4。将这两个直角三角形按图1所示位置摆放，其中直角边在同一直线上，且点与点重合。现固定，将以每秒1个单位长度的速度在上向右平移，当点与点重合时运动停止。设平移时间为秒。

    （1）当为       秒时，边恰好经过点；当为       秒时，运动停止；
    （2）在平移过程中，设与重叠部分的面积为，请直接写出与的函数关系式，并写出的取值范围；
    （3）当停止运动后，如图2，为线段上一点，若一动点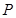从点出发，先沿方向运动，到达点后再沿斜坡方向运动到达点，若该动点在线段上运动的速度是它在斜坡上运动速度的2倍，试确定斜坡的坡度，使得该动点从点运动到点所用的时间最短。（要求，简述确定点位置的方法，但不要求证明。）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图1，已知抛物线y=ax2+bx（a≠0）经过A（3，0）、B（4，4）、D(2, n)三点．

    （1）求抛物线的解析式及点D坐标；
    （2）点M是抛物线对称轴上一动点，求使BM－AM的值最大时的点M的坐标；
    （3）如图2，将射线BA沿BO翻折，交y轴于点C，交抛物线于点N，求点N的坐标；
    (4)在（3）的条件下，连结ON,OD，如图2，请求出所有满足△POD∽△NOB的点P坐标（点P、O、D分别与点N、O、B对应）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，抛物线与轴交于点A(－1，0)、B(3，0)，与轴交于点C(0，3)．

    (1)求抛物线的解析式及顶点D的坐标；
    (2)若P为线段BD上的一个动点，点P的横坐标为m，试用含m的代数式表示点P的纵坐标；
    (3)过点P作PM⊥x轴于点M，求四边形PMAC的面积的最大值和此时点P的坐标；
    (4)若点F是第一象限抛物线上的一个动点，过点F作FQ∥AC交x轴于点Q．当点F的坐标为          时，四边形FQAC是平行四边形；当点F的坐标为           时，四边形FQAC是等腰梯形(直接写出结果，不写求解过程)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，直线y=x+3与坐标轴分别交于A，B两点，抛物线y=ax2+bx﹣3a经过点A，B，顶点为C，连接CB并延长交x轴于点E，点D与点B关于抛物线的对称轴MN对称．


    （1）求抛物线的解析式及顶点C的坐标；
    （2）求证：四边形ABCD是直角梯形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    在平面直角坐标系xOy中，一块含60°角的三角板作如图摆放，斜边AB在x轴上，直角顶点C在y轴正半轴上，已知点A（-1，0）．

    （1）请直接写出点B，C的坐标：B（  ，  ），C（  ，  ）；
    （2）求经过A，B，C三点的抛物线解析式；
    （3）现有与上述三角板完全一样的三角板DEF（其中∠EDF=90°，∠DEF=60°），把顶点E放在线段AB上（点E是不与A，B两点重合的动点），并使ED所在直线经过点C．此时，EF所在直线与（2）中的抛物线交于第一象限的点M．当AE=2时，抛物线的对称轴上是否存在点P使△PEM是等腰三角形，若存在，请求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图，抛物线y=ax2+bx（a＞0）经过原点O和点A（2，0）．

    （1）写出抛物线的对称轴与x轴的交点坐标；
    （2）点（x1，y1），（x2，y2）在抛物线上，若x1＜x2＜1，比较y1，y2的大小；
    （3）点B（﹣1，2）在该抛物线上，点C与点B关于抛物线的对称轴对称，求直线AC的函数关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    矩形纸片ABCD中，AB=5，AD=4．
    （1）如图1，四边形MNEF是在矩形纸片ABCD中裁剪出的一个正方形．你能否在该矩形中裁剪出一个面积最大的正方形，最大面积是多少？说明理由；

    （2）请用矩形纸片ABCD剪拼成一个面积最大的正方形．要求：在图2的矩形ABCD中画出裁剪线，并在网格中画出用裁剪出的纸片拼成的正方形示意图（使正方形的顶点都在网格的格点上）．

    查看答案和解析>>

    同步练习册答案