
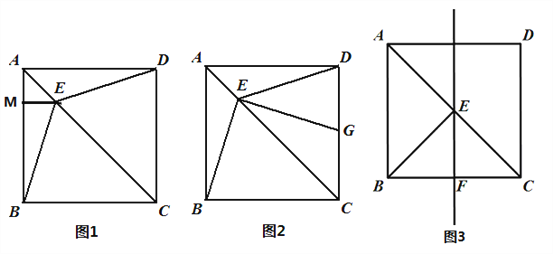
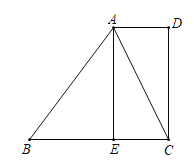
����Ŀ����ͼ����������ABCD�У�AB=4����E�ڶԽ���AC�ϣ�����BE��DE��
��1����ͼ1����EM��AB��AB�ڵ�M����AE=![]() ʱ����BE�ij���
ʱ����BE�ij���
��2����ͼ2����EG��BE��CD�ڵ�G����֤��BE=EG��
��3����ͼ3����EF��BC��BC�ڵ�F����BF=x����BEF�����Ϊy����xȡ��ֵʱ��yȡ�����ֵ�����ֵ�Ƕ��٣�����BEF�����ȡ�����ֵʱ����ֱ��EFȡ��P������BP��PC��ʹ�á�BPC=45������EP�ij�����
���𰸡�(1) ![]() (2)������(3)
(2)������(3) ![]()
�������������������1������E��EM��AB����AB�ڵ�M����AM=EM=1�����ɹ��ɶ������BE=![]() ��
��
��2����֤��BCE�ա�DCE����BE=DE������֤����EDG=��EGD����EG=ED���Ӷ��ó����ۣ�
��3�����������������ʽ�ú�����ϵʽ![]() ���Ӷ��ó�����.
���Ӷ��ó�����.
�����������1������E��EM��AB����AB�ڵ�M��
��AE=![]() ������AM=EM=1��
������AM=EM=1��
��BM=3��
��BE=![]()
��2����֤��BCE�ա�DCE��
�� BE=DE����CBE=��CDE
��EG��BE����BCD=90����
���CBE+��CGE=��CGE+��EGD=180��
���CBE=��EGD
���EDG=��EGD
��EG=ED
��EG=BE
��3��![]()
��![]() ʱ��
ʱ��
![]()
��ͼ��������á�EPC=��ECP=22.5����
��PE=CE=![]() ��
��
![]()




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ������6��3��4��7��6��3��5��6����
��1���������ݵ�ƽ��������������λ����
��2���������ݵķ���ͱ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
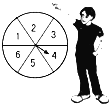
����Ŀ����ͼ��ʾ��ת�̱��ȷֳ��������Σ���������һ��д������1��2��3��4��5��6��������ת��ת�̣�����ֹͣת��ʱ����
��1��ָ��ָ��4�ĸ��ʣ�
��2��ָ��ָ�������������ĸ��ʣ�
��3��ָ��ָ�����ֲ�С��5�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϲ�����й����⣺
����֪����|x|��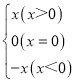 ���������ǿ�������һ�����������о���ֵ�Ĵ���ʽ���绯�����ʽ|x+1|+|x��2|ʱ������x+1��0��x��2��0���ֱ����x����1��x��2���Ʃ�1��2�ֱ�Ϊ|x+1|��|x��2|�����ֵ������ʵ����Χ�ڣ����ֵx����1��x��2�ɽ�ȫ��ʵ���ֳɲ��ظ��Ҳ���©������3���������x����1���ک�1��x��2����x��2��
���������ǿ�������һ�����������о���ֵ�Ĵ���ʽ���绯�����ʽ|x+1|+|x��2|ʱ������x+1��0��x��2��0���ֱ����x����1��x��2���Ʃ�1��2�ֱ�Ϊ|x+1|��|x��2|�����ֵ������ʵ����Χ�ڣ����ֵx����1��x��2�ɽ�ȫ��ʵ���ֳɲ��ظ��Ҳ���©������3���������x����1���ک�1��x��2����x��2��
�Ӷ��������ʽ|x+1|+|x��2|�ɷ�����3�������
�ٵ�x����1ʱ��ԭʽ������x+1������x��2������2x+1��
�ڵ���1��x��2ʱ��ԭʽ��x+1����x��2����3��
�۵�x��2ʱ��ԭʽ��x+1+x��2��2x��1��
�������ۣ�ԭʽ��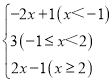
ͨ�������Ķ����������������⣺
��1����x��2ʱ��|x��2|���� ����
��2�����ݲ����еķ����������ʽ|x+2|+|x��4|����д�������̣�
��3��ֱ��д��|x��1|��4|x+1|�����ֵ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������O�У�ֱ��AB��ֱ��CD��E������A����DAF=��DAB������D��AF�Ĵ��ߣ�����ΪF����AB���ӳ����ڵ�P������CO���ӳ�����O�ڵ�G������EG��
��1����֤��DF����O�����ߣ�
��2����AD=DP��OB=3����![]() �ij��ȣ�
�ij��ȣ�
��3����DE=4��AE=8�����߶�EG�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ABC=��ACB����ACΪֱ������O�ֱ�AB��BC�ڵ�M��N����P��AB���ӳ����ϣ�����CAB=2��BCP��
��1����֤��ֱ��CP����O�����ߣ�
��2����BC=2![]() ��sin��BCP=
��sin��BCP=![]() �����B��AC�ľ��룮
�����B��AC�ľ��룮
��3���ڵڣ�2���������£�����ACP���ܳ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ң���1��ͼ��1���������Ρ�6�������κ�6���ȱ��������������2��ͼ��2���������Ρ�11�������κ�10���ȱ���������ɣ���3��ͼ��3���������Ρ�16�������κ�14���ȱ�����������������մ˹��ɣ���![]() ��ͼ�������κ͵ȱ������εĸ���֮��Ϊ ��.
��ͼ�������κ͵ȱ������εĸ���֮��Ϊ ��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���ACB=90�㣬AB=5cm��BC=3cm������P�ӵ�A��������ÿ��2cm���ٶ�������A��C��B��A�˶������˶�ʱ��Ϊt�루t��0����

(1)����P��AC�ϣ�������PA=PBʱ�������ʱt��ֵ��
(2)����Pǡ���ڡ�BAC�Ľ�ƽ�����ϣ���t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�![]() ��EΪ��BC��һ�㣬��EC=AD������AC.
��EΪ��BC��һ�㣬��EC=AD������AC.
��1����֤���ı���AECD�Ǿ��Σ�
��2����ACƽ�֡�DAB��AB=5��EC=2����AE�ij���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com