
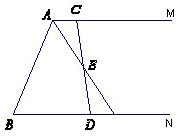
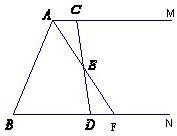
 解:(1)∵AM∥BN,
解:(1)∵AM∥BN,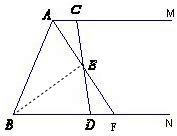 连接BE.
连接BE.

科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 ;(直接写结果)
;(直接写结果)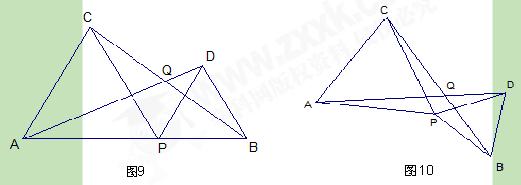
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(广西区南宁卷)数学 题型:解答题
(本题满分9分)如图9,已知线段AB的长为2a,点P是AB上的动点(P不与A,B重合),分别以AP、PB为边向线段AB的同一侧作正△APC和正△PBD.
(1)当△APC与△PBD的面积之生取最小值时,AP= ;(直接写结果)
;(直接写结果)
(2)连结AD、BC,相交于点Q,设∠AQC=α,那么α的大小是否会随点P的移动面变化?请说明理由;
(3)如图10,若点P固定,将△PBD绕点P按顺时针方向旋转(旋转角小于 180°),此时α的大小是否发生变化?(只需直接写出你的猜想,不必证明)
180°),此时α的大小是否发生变化?(只需直接写出你的猜想,不必证明)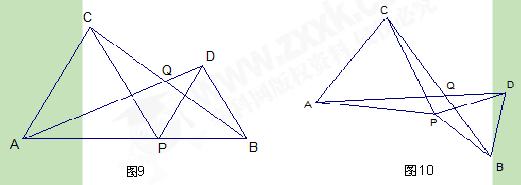
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com