
 将矩形纸片ABCD按如图方式折叠,使点D与点B重合,点C落在点C′处.折痕为EF,若S△ABE:S四边形ABFE=4:9,则cos∠BEF=( )
将矩形纸片ABCD按如图方式折叠,使点D与点B重合,点C落在点C′处.折痕为EF,若S△ABE:S四边形ABFE=4:9,则cos∠BEF=( )| A. | $\frac{1}{3}$ | B. | $\frac{3\sqrt{10}}{10}$ | C. | 3 | D. | $\frac{\sqrt{10}}{10}$ |
分析 由S△ABE:S四边形ABFE=4:9,可知AE:BF=4:5,然后由平行线的性质和翻折的性质可知:∠BEF=∠BFE,从而得到BE=BF,设AE=4x,则BE=BF=5x,在Rt△ABE中,由勾股定理得;AB=3x,接下来证明四边形ABFG为矩形,得到GE=x,在△EGF中,EF=$\sqrt{10}x$,从而可求得cos∠BEF=$\frac{\sqrt{10}}{10}$.
解答 解:如图所示,过点F作FG⊥AD,垂足为G.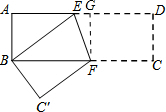
∵S△ABE:S四边形ABFE=4:9,
∴S△AEB:SBEF=4:5.
∴AE:BF=4:5.
∵AD∥BC,
∴∠DEF=∠EFB.
由翻折的性质可知:∠DEF=∠BEF.
∴∠BEF=∠BFE.
∴BE=BF.
设AE=4x,则BE=BF=5x,
在Rt△ABE中,由勾股定理得;$AB=\sqrt{B{E}^{2}-A{E}^{2}}=3x$.
∵∠A=∠ABF=∠FGA=90°,
∴四边形ABFG为矩形,
∴GF=AB=3x.AG=BF=5x.
∴GE=AG-AE=5x-4x=x.
在△EGF中,EF=$\sqrt{E{G}^{2}+F{G}^{2}}$=$\sqrt{10}x$.
∴cos∠FEG=$\frac{EG}{EF}=\frac{x}{\sqrt{10}x}=\frac{\sqrt{10}}{10}$.
∴cos∠BEF=$\frac{\sqrt{10}}{10}$.
故选:D.
点评 本题主要考查的是翻折的性质、勾股定理、矩形的性质和判定,证得BF=BE,然后由勾股定理求得AB的长是解题的关键.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:选择题
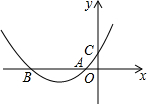 如图,抛物线y=ax2+bx+c与坐标轴的交点为A、B、C,且OA=OC=1,则下列关系中正确的是( )
如图,抛物线y=ax2+bx+c与坐标轴的交点为A、B、C,且OA=OC=1,则下列关系中正确的是( )| A. | a+b=-1 | B. | ac<0 | C. | b<2a | D. | a-b=-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两个正方形是相似图形 | |
| B. | 两个菱形是相似图形 | |
| C. | 底角相等的两个等腰三角形是相似图形 | |
| D. | 顶角相等的两个等腰三角形是相似图形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
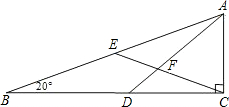 如图,在△ABC中,∠ACB=90°,D在BC上,E是AB的中点,AD、CE相交于F,且AD=DB.若∠B=20°,则∠DFE等于( )
如图,在△ABC中,∠ACB=90°,D在BC上,E是AB的中点,AD、CE相交于F,且AD=DB.若∠B=20°,则∠DFE等于( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com