【题目】如图，等边三角形△ABC的边长为4，过点C的直线
⊥AC，且△ABC与△A′B′C关于直线对称，D为线段BC′上一动点，则AD+BD的最小值是______；
【答案】8
【解析】连接BB/，根据△ABC、△A/CB/均为正三角形即可得出A/CBB/为菱形，进而得出点B关于CB/对称的点A/，以此确定点D与点C重合时，AD+BD的最小，代入数据即可得出结论.
解：连接BB/，如图所示.
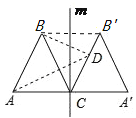
∵△ABC、△A/CB/ /均为正三角形，
∴∠ACB=∠A/=60°，A/C=BC=A/B/，
∴A/B/∥BC，
∴四边形A/CBB/ /为菱形，
∴点B关于CB/对称的点A/，
∴当点D与点C重合时，AD+BD取最小值，
此时AD+BD=4+4=8.
故答案为：8.
“点睛”本题考查了轴对称中的最短线路问题以及等边三角形的性质，找出点B关于CB/对称的点A/是解题的关键.
科目：初中数学 来源： 题型：
【题目】已知：点O到△ABC的两边AB，AC所在直线的距离相等，且OB=OC．
（1）如图1，若点O在边BC上，过点O分别作OE⊥AB，OF⊥AC，E，F分别是垂足．
判断
与
的关系______；
（2）如图2，若点O在△ABC的内部，求证：AB=AC；
（3）若点O在△ABC的外部，AB=AC一定成立吗？请画图表示，不需证明．
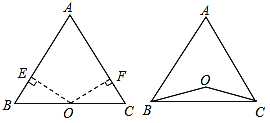
图1 图2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，已知抛物线的方程C1： 
(m＞0)与x轴交于点B、C，与y轴交于点E，且点B在点C的左侧．
（1）若抛物线C1过点M(2, 2)，求实数m的值；
（2）在（1）的条件下，求△BCE的面积；
（3）在（1）的条件下，在抛物线的对称轴上找一点H，使得BH＋EH最小，求出点H的坐标；
（4）在第四象限内，抛物线C1上是否存在点F，使得以点B、C、F为顶点的三角形与△BCE相似？若存在，求m的值；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）如图1，已知锐角△ABC中，分别以AB、AC为边向△ABC外作等边△ABD和等边△ACE，连结BE、CD，则线段BE与线段CD的数量关系是______．
（2）如图2，已知锐角△ABC中，分别以AB、AC为边向△ABC外作等腰直角△ABD和等腰直角△ACE，连结BE、CD，猜想线段BE与线段CD的有什么位置关系？并证明你的猜想．
（3）如图3，已知锐角△ABC中，分别以AB、AC为边向△ABC外作正方形ABDE和正方形ACFG，连接CE、BG，请写出线段CE与线段BG有什么关系？不需证明．
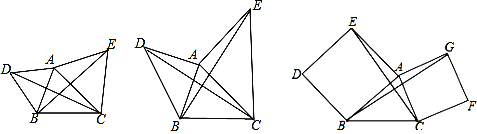
图1 图2 图3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在直线
上，点
在
、
两点之间，点
为线段
的中点，点
为线段
的中点．若
，且
使关于
的方程
有无数个解．
（1）求线段
的长；
（2）试说明线段
的长与点
在线段
上的位置无关；
（3）如图，若点
为线段
的中点，点
在线段
的延长线上，试说明
的值不变．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com