
 已知正方形OABC的面积为4,点O是坐标原点,点A在x轴上,点C在y轴上,点B在函数y=$\frac{k}{x}$(x>0,k>0)的图象上,点P(m,n)是函数y=$\frac{k}{x}$(x>0,k>0)的图象上任意一点.过点P分别作x轴、y轴的垂线,垂足分别为E、F.若设矩形OEPF和正方形OABC不重合部分的面积为S.
已知正方形OABC的面积为4,点O是坐标原点,点A在x轴上,点C在y轴上,点B在函数y=$\frac{k}{x}$(x>0,k>0)的图象上,点P(m,n)是函数y=$\frac{k}{x}$(x>0,k>0)的图象上任意一点.过点P分别作x轴、y轴的垂线,垂足分别为E、F.若设矩形OEPF和正方形OABC不重合部分的面积为S.分析 (1)由正方形的性质得出OA=OC=AB=BC=2,从而得出点B坐标,而点B在双曲线上,求出k;
(2)先求出矩形CDPF的面积,借助双曲线的性质得出S的函数关系式,又有mn=4,联立方程组求出点P的坐标.
(3)分两种情况,先求出点D的坐标,进而求出四边形OCDE的面积,用面积之差即可得出结论.
解答 解:(1)∵正方形ABCD的面积为4,
∴OA=AB=BC=OC=2,
∴B(2,2),
∵点B在函数y=$\frac{k}{x}$(x>0,k>0)的图象上,
∴k=2×2=4,
(2)如图,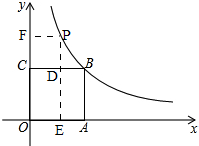
由(1)知,点B(4,4)
∴PF=|m-4|,PD=PC=|n-4|,
∴S矩形FCDP=|m-4|×|n-4|=|(m-4)(n-4)|=(m-4)(4-n),
由双曲线的性质,得,S=2S矩形FCDP=2(m-4)(4-n),
∵S=$\frac{8}{3}$,
∴2(m-4)(4-n)=$\frac{8}{3}$①
由(1)知,mn=4②,
联立①②得,$\left\{\begin{array}{l}{m=\frac{4}{3}}\\{n=3}\end{array}\right.$或$\left\{\begin{array}{l}{m=3}\\{n=\frac{4}{3}}\end{array}\right.$,
∴P($\frac{4}{3}$,3)或(3,$\frac{4}{3}$)
(3)
当0<m≤2时,∵B(2,2),P(m,n),
∴D(m,2),∴OE=m,OC=2,
∴∴S四边形OCDE=OE×OC=2m,
∴S=2(S四边形OABC-S四边形OCDE)=2(4-2m)=8-4m,
当m>2时,同(1)的方法得,S=8-$\frac{16}{m}$
点评 此题是反比例函数综合题,主要考查了正方形的性质,矩形的性质,双曲线的性质,解本题的关键是求出矩形FCDP的面积.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:选择题
 如图,小颖利用一个锐角是30°的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5m,AB为1.5m(即小颖的眼睛距地面的距离),那么这棵树高是( )
如图,小颖利用一个锐角是30°的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5m,AB为1.5m(即小颖的眼睛距地面的距离),那么这棵树高是( )| A. | 4m | B. | $\frac{5\sqrt{3}}{3}$m | C. | (5$\sqrt{3}$+$\frac{3}{2}$)m | D. | ($\frac{5\sqrt{3}}{3}$+$\frac{3}{2}$)m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 288元 | B. | 332元 | C. | 288元或316元 | D. | 332元或363元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,边长为1的小正方形网格中,⊙O的圆心在格点上,则sin∠EDB的值是( )
如图,边长为1的小正方形网格中,⊙O的圆心在格点上,则sin∠EDB的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{2}}{5}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 锐角△ABC中,已知∠B>∠C,I为内心,R为外接圆半径,AD为边BC上的高线,点K在直线AD上,满足AK=2R,证明:∠KID=$\frac{∠B-∠C}{2}$.
锐角△ABC中,已知∠B>∠C,I为内心,R为外接圆半径,AD为边BC上的高线,点K在直线AD上,满足AK=2R,证明:∠KID=$\frac{∠B-∠C}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | $\frac{5}{4}$ | B. | $\frac{4}{3}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 电子跳蚤游戏盘如图所示的△ABC,AB=8,AC=9,BC=10,如果跳蚤开始时在BC边的点P0处,BP0=4.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;跳蚤按上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2015与A间的距离为( )
电子跳蚤游戏盘如图所示的△ABC,AB=8,AC=9,BC=10,如果跳蚤开始时在BC边的点P0处,BP0=4.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;跳蚤按上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2015与A间的距离为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com