
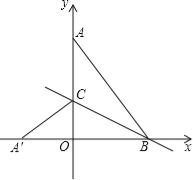
【题目】如图,在平面直角坐标系中,点A(0,4),B(3,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,则直线BC的解析式为 .
【答案】y=﹣![]() x+
x+![]()
【解析】
在Rt△OAB中,OA=4,OB=3,用勾股定理计算出AB=5,再根据折叠的性质得BA′=BA=5,CA′=CA,则OA′=BA′﹣OB=2,设OC=t,则CA=CA′=4﹣t,在Rt△OA′C中,根据勾股定理得到t2+22=(4﹣t)2,解得t=![]() ,则C点坐标为(0,
,则C点坐标为(0,![]() ),然后利用待定系数法确定直线BC的解析式
),然后利用待定系数法确定直线BC的解析式
解:∵A(0,4),B(3,0),
∴OA=4,OB=3,
在Rt△OAB中,AB=![]() =5,
=5,
∵△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,
∴BA′=BA=5,CA′=CA,
∴OA′=BA′﹣OB=5﹣3=2,
设OC=t,则CA=CA′=4﹣t,
在Rt△OA′C中,
∵OC2+OA′2=CA′2,
∴t2+22=(4﹣t)2,解得t=![]() ,
,
∴C点坐标为(0,![]() ),
),
设直线BC的解析式为y=kx+b,
把B(3,0)、C(0,![]() )代入得
)代入得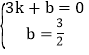 ,解得
,解得
∴直线BC的解析式为y=﹣![]() x+
x+![]()
故答案为:y=﹣![]() x+
x+![]() .
.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案科目:初中数学 来源: 题型:
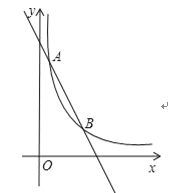
【题目】如图,一次函数y=kx+b与反比例函数![]() 的图象交于点A(1,6),B(3,n)两点.
的图象交于点A(1,6),B(3,n)两点.
(1)求一次函数的表达式;
(2)在y轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
(1)求证:AC平分∠DAB;
(2)求证:△PCF是等腰三角形;
(3)若∠BEC=30°,求证:以BC,BE,AC边的三角形为直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:小聪遇到这样一个问题: 如图1,![]() ,请画一个
,请画一个![]() ,使
,使![]() 与
与![]() 互补.
互补.

小聪是这样思考的:首先通过分析明确射线![]() 在
在![]() 的外部,画出示意图,如图2所示:然后通过构造平角找到
的外部,画出示意图,如图2所示:然后通过构造平角找到![]() 的补角
的补角![]() ,
,

如图3所示:进而分析要使![]() 与
与![]() 互补,则需
互补,则需![]() .
.

因此,小聪找到了解决问题的方法:反向延长射线![]() 得到射线
得到射线![]() ,利用量角器画出
,利用量角器画出![]() 的平分线
的平分线![]() ,这样就得到了
,这样就得到了![]() 与
与![]() 互补
互补
(1)小聪根据自己的画法写出了己知和求证,请你完成证明.已知:如图3,点![]() 在直线
在直线![]() 上,射线
上,射线![]() 平分
平分![]() .求证:
.求证: ![]() 与
与![]() 互补. .
互补. .

(2)参考小聪的画法,请在下图中画出--个![]() ,使
,使![]() 与
与![]() 互余.(保留画图痕迹)
互余.(保留画图痕迹)

(3)已知![]() 和
和![]() 互余,射线
互余,射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() .若
.若![]() ,直接写出锐角
,直接写出锐角![]() 的度数是 .
的度数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,老师给出了如下问题:

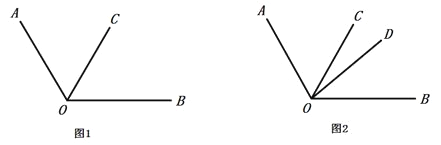
(1)以下是小刚的解答过程,请你将解答过程补充完整:
解:如图2,因为![]() ,
,![]() 平分
平分![]() ,
,
所以![]() ______
______![]() ______
______![]() (角平分线的定义).
(角平分线的定义).
因为![]() ,
,
所以![]() ______
______![]() .
.
(2)小戴说:“我觉得这道题有两种情况,小刚考虑的是![]() 在
在![]() 内部的情况,事实上,
内部的情况,事实上,![]() 还可能在
还可能在![]() 的内部”.根据小戴的想法,请你在图1中画出另一种情况对应的图形,并直接写出
的内部”.根据小戴的想法,请你在图1中画出另一种情况对应的图形,并直接写出![]() 的度数:______.
的度数:______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京张高铁是2022年北京冬奥会的重要交通保障设施. 如图所示,京张高铁起自北京北站,途经清河、沙河、吕平等站,终点站为张家口南站,全长174千米.
(1)根据资料显示,京张高铁的客运价格拟定为0. 4元(人·千米),可估计京张高铁单程票价约为_________元(结果精确到个位);
(2)京张高铁建成后,将是世界上第一条设计时速为350千米/时的高速铁路. 乘高铁从北京到张家口的时间将缩短至1小时,如果按此设计时速运行,那么每站(不计起始站和终点站)停靠的平均时间是多少分钟?(结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在平行四边形ABCD中,BC=2AB,CE⊥AB于E,F为AD的中点,若∠AEF=54,则∠B=( )

A. 54 B. 60 C. 72 D. 66
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中AB∥CD,对角线AC,BD相交于O,点E,F分别为BD上两点,且BE=DF,∠AEF=∠CFB.
(1)求证:四边形ABCD是平行四边形;
(2)若AC=2OE,试判断四边形AECF的形状,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com