
 如图,菱形ABCD中,分别延长DC,BC至点E、F,使CE=CD,CF=CB,连接DB,BE,EF,FD,如果∠A=60°,DF的长为8$\sqrt{3}$,则菱形ABCD的面积为( )
如图,菱形ABCD中,分别延长DC,BC至点E、F,使CE=CD,CF=CB,连接DB,BE,EF,FD,如果∠A=60°,DF的长为8$\sqrt{3}$,则菱形ABCD的面积为( )| A. | 8$\sqrt{3}$ | B. | 16$\sqrt{3}$ | C. | 32$\sqrt{3}$ | D. | 64$\sqrt{3}$ |
分析 先连接AC,交BD于G,构造含30°角的直角三角形,再根据CG是△BDF的中位线,求得GC的长和DG的长,最后根据菱形ABCD的面积=$\frac{1}{2}$×AC×BD,进行计算即可.
解答 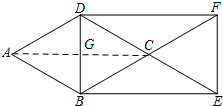 解:连接AC,交BD于G,则∠DGC=90°,G是BD的中点,
解:连接AC,交BD于G,则∠DGC=90°,G是BD的中点,
∵菱形ABCD中,∠A=60°,
∴∠DCG=30°,
∵CF=CB,BG=GD,
∴CG是△BDF的中位线,
∴GC=$\frac{1}{2}$DF=$\frac{1}{2}$×8$\sqrt{3}$=4$\sqrt{3}$,
∴DG=$\frac{GC}{\sqrt{3}}$=4,
∴BD=8,AC=8$\sqrt{3}$,
∴菱形ABCD的面积=$\frac{1}{2}$×AC×BD=$\frac{1}{2}$×8$\sqrt{3}$×8=32$\sqrt{3}$.
故选(C)
点评 本题主要考查了菱形的性质,解题时注意:菱形的对角线互相垂直平分,菱形面积等于两条对角线的长度乘积的一半.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点A(p,q)(0<p<q)在反比例函数y=$\frac{3}{x}$的图象上,且OA=5,过A作AC⊥y轴垂足为C,线段OA的垂直平分线交OC于点B,连结AB,则△ABC的周长为( )
如图,点A(p,q)(0<p<q)在反比例函数y=$\frac{3}{x}$的图象上,且OA=5,过A作AC⊥y轴垂足为C,线段OA的垂直平分线交OC于点B,连结AB,则△ABC的周长为( )| A. | 8 | B. | 7 | C. | 2$\sqrt{7}$ | D. | $\sqrt{31}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
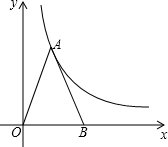 如图所示,如果△ABO的面积为6,且AO=AB,双曲线y=$\frac{k}{x}$(k≠0)经过点A,则k的值为( )
如图所示,如果△ABO的面积为6,且AO=AB,双曲线y=$\frac{k}{x}$(k≠0)经过点A,则k的值为( )| A. | 3 | B. | -3 | C. | 6 | D. | -6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 阅读以下材料:对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:
阅读以下材料:对于三个数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com