
【题目】在平面直角坐标系xOy中,已知抛物线G:y=ax2﹣2ax+4(a≠0).
(1)当a=1时,
①抛物线G的对称轴为x= ;
②若在抛物线G上有两点(2,y1),(m,y2),且y2>y1,则m的取值范围是 ;
(2)抛物线G的对称轴与x轴交于点M,点M与点A关于y轴对称,将点M向右平移3个单位得到点B,若抛物线G与线段AB恰有一个公共点,结合图象,求a的取值范围.
【答案】(1)①1;②m>2或m<0;(2)﹣![]() <a≤﹣
<a≤﹣![]() 或a=4.
或a=4.
【解析】
(1)当a=1时,①根据二次函数一般式对称轴公式![]() ,即可求得抛物线G的对称轴;
,即可求得抛物线G的对称轴;
②根据抛物线的对称性求得![]() 关于对称轴
关于对称轴![]() 的对称点为
的对称点为![]() ,再利用二次函数图像的增减性即可求得答案;
,再利用二次函数图像的增减性即可求得答案;
(2)根据平移的性质得出![]() 、
、![]() ,由题意根据函数图象分三种情况进行讨论,即可得解.
,由题意根据函数图象分三种情况进行讨论,即可得解.
解:(1)①∵当a=1时,抛物线G:y=ax2﹣2ax+4(a≠0)为:![]()
∴抛物线G的对称轴为![]() ;
;
②画出函数图象:
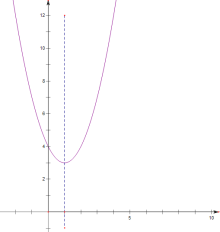
∵在抛物线G上有两点(2,y1),(m,y2),且y2>y1,![]() ,
,
∴①当![]() 时,
时,![]() 随
随![]() 的增大而增大,此时有
的增大而增大,此时有![]() ;②当
;②当![]() 时,
时,![]() 随
随![]() 的增大而减小,抛物线G上点
的增大而减小,抛物线G上点![]() 关于对称轴
关于对称轴![]() 的对称点为
的对称点为![]() ,此时有
,此时有![]() .
.
∴m的取值范围是![]() 或
或![]() ;
;
(2)∵抛物线G:y=ax2﹣2ax+4(a≠0的对称轴为x=1,且对称轴与x轴交于点M
∴点M的坐标为(1,0)
∵点M与点A关于y轴对称
∴点A的坐标为(﹣1,0)
∵点M右移3个单位得到点B
∴点B的坐标为(4,0)
依题意,抛物线G与线段AB恰有一个公共点
把点A(﹣1,0)代入y=ax2﹣2ax+4,可得![]() ;
;
把点B(4,0)代入y=ax2﹣2ax+4,可得![]() ;
;
把点M(1,0)代入y=ax2﹣2ax+4,可得a=4.

根据所画图象可知抛物线G与线段AB恰有一个公共点时可得:![]() 或
或![]() .
.
故答案是:(1)①1;②m>2或m<0;(2)![]() 或
或![]()


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c的图象,下列结论:①2a>b;②a﹣b+c>0;③a<b;④a>c,其中正确的结论是( )
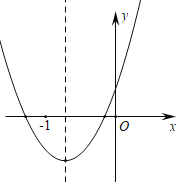
A.①③B.②③C.①④D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
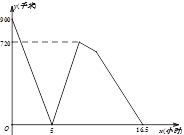
【题目】甲、乙两车分别从![]() 、
、![]() 两地同时出发,相向行驶,已知甲车的速度大于乙车的速度,甲车到达
两地同时出发,相向行驶,已知甲车的速度大于乙车的速度,甲车到达![]() 地后马上以另一速度原路返回
地后马上以另一速度原路返回![]() 地(掉头的时间忽略不计),乙车到达
地(掉头的时间忽略不计),乙车到达![]() 地以后即停在
地以后即停在![]() 地等待甲车.如图所示为甲乙两车间的距离
地等待甲车.如图所示为甲乙两车间的距离![]() (千米)与甲车的行驶时间
(千米)与甲车的行驶时间![]() (小时)之间的函数图象,则当乙车到达
(小时)之间的函数图象,则当乙车到达![]() 地的时候,甲车与
地的时候,甲车与![]() 地的距离为__________千米.
地的距离为__________千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=4,点E是A边上一点,且AE=![]() ,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.
,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.
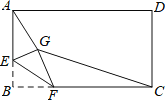
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是AB上一点,连接DE.过点A作AF⊥DE,垂足为F,⊙O经过点C、D、F,与AD相交于点G.
(1)求证:△AFG∽△DFC;
(2)若正方形ABCD的边长为4,AE=1,求⊙O的半径.
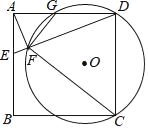
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年初,新型冠状病毒肺炎侵袭湖北,武汉是重灾区,某爱心人士两次购买N95口罩支援武汉,第一次花了500000元,第二次花了770000,购买了同样的N95口罩,已知第二次购买的口罩的单价是第一次的1.4倍,且比第一次多购进了10000个,求该爱心人士第一次购进口罩的单价.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小元步行从家去火车站,走到 6 分钟时,以同样的速度回家取物品,然后从家乘出租车赶往火车站,结果比预计步行时间提前了3 分钟.小元离家路程S(米)与时间t(分钟)之间的函数图象如图,从家到火车站路程是( )

A.1300 米B.1400 米C.1600 米D.1500 米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一动点从半径为2的![]() 上的
上的![]() 点出发,沿着射线
点出发,沿着射线![]() 方向运动到
方向运动到![]() 上的点
上的点![]() 处,再向左沿着与射线
处,再向左沿着与射线![]() 夹角为
夹角为![]() 的方向运动到
的方向运动到![]() 上的点
上的点![]() 处;接着又从
处;接着又从![]() 点出发,沿着射线
点出发,沿着射线![]() 方向运动到
方向运动到![]() 上的点
上的点![]() 处,再向左沿着与射线
处,再向左沿着与射线![]() 夹角为
夹角为![]() 的方向运动到
的方向运动到![]() 上的点
上的点![]() 处;
处;![]() 间的距离是________;…按此规律运动到点
间的距离是________;…按此规律运动到点![]() 处,则点
处,则点![]() 与点
与点![]() 间的距离是________.
间的距离是________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com