
【题目】如图,抛物线y=a(x﹣![]() )(x+3)交x轴于点A、B,交y轴于点C,tan∠CAO=
)(x+3)交x轴于点A、B,交y轴于点C,tan∠CAO=![]() .
.
(1)求a值;
(2)点P为第一象限内抛物线上一点,点P的横坐标为t,连接PA,PC,设△PAC的面积为S,求S与t之间的关系式;
(3)在(2)的条件下,点Q在第一象限内的抛物线上(点Q在点P的上方),过点P作PE⊥AB,垂足为E,点D在线段AQ上,点F在线段AO上连接ED、DF,DE交AP于点G,若∠QDF+∠QDE=180°,∠DFA+∠AED=90°,PG=PE,PG:EF=3:2,求点P的坐标.

【答案】(1)a=﹣![]() ;(2)S=
;(2)S=![]() t2+
t2+![]() t;(3)点P(1,3)
t;(3)点P(1,3)
【解析】
(1)由题意可求点A,点B坐标,由锐角三角函数可求点C坐标,代入解析式可求解a的值;
(2)点P(t,﹣![]() t2﹣
t2﹣![]() t+4),由面积关系可求解;
t+4),由面积关系可求解;
(3)如图3,延长AQ,EP交于点H,连接GF,由四点共圆可证点A,点D,点G,点F四点共圆,可得∠ADF=∠AGF,∠QDE=∠AFG,设PG=PE=3a,EF=2a,由勾股定理可求a=![]() ,可求点P坐标,代入解析式可求解.
,可求点P坐标,代入解析式可求解.
解:(1)∵抛物线y=a(x﹣![]() )(x+3)交x轴于点A、B,
)(x+3)交x轴于点A、B,
∴0=a(x﹣![]() )(x+3)
)(x+3)
∴x1=![]() ,x2=﹣3,
,x2=﹣3,
∴点A(﹣3,0),点B(![]() ,0),
,0),
∴AO=3,
∵tan∠CAO=![]() =
=![]() ,
,
∴CO=4,
∴点C(0,4)
∴4=a(0﹣![]() )(0+3),
)(0+3),
∴a=﹣![]()
(2)∵y=﹣![]() (x﹣
(x﹣![]() )(x+3)
)(x+3)
∴y=﹣![]() x2﹣
x2﹣![]() x+4,
x+4,
∵点P的横坐标为t,
∴点P(t,﹣![]() t2﹣
t2﹣![]() t+4),
t+4),
∴S=![]() [4+(﹣
[4+(﹣![]() t2﹣
t2﹣![]() x+4)]t+
x+4)]t+![]() ×3×4﹣
×3×4﹣![]() ×(t+3)(﹣
×(t+3)(﹣![]() t2﹣
t2﹣![]() t+4)=
t+4)=![]() t2+
t2+![]() t;
t;
(3)如图3,延长AQ,EP交于点H,连接GF,
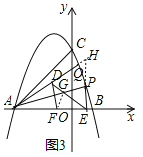
∵∠QDF+∠QDE=180°,且∠QDE+∠ADE=180°,
∴∠ADE=∠QDF,
∴∠ADF=∠QDE,
∵∠DFA+∠AED=90°,∠AED+∠DEP=90°,
∴∠AFD=∠DEP,
∴∠HAE=∠AHE,且HE⊥AE,
∴∠HAE=∠AHE=45°,
∴AE=EH=t+3,
∵PE=PG,
∴∠PGE=∠PEG,
∴∠PGE=∠AFD=∠AGD,
∴点A,点D,点G,点F四点共圆,
∴∠ADF=∠AGF,∠QDE=∠AFG,
∴∠AGF=∠AFG,
∴AF=AG,
设PG=PE=3a,EF=2a,
∴AF=t+3﹣2a=AG,AP=t+3﹣2a+3a=t+3+a,
∵AP2=PE2+AE2,
∴(t+3+a)2=9a2+(t+3)2,
∴a=![]() ,
,
∴3a=![]()
∴点P(t,![]() )
)
∴![]() =﹣
=﹣![]() t2﹣
t2﹣![]() t+4,
t+4,
∴t=1,t=﹣3(不合题意舍去)
∴点P(1,3)


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 是线段
是线段![]() 上的动点,将线段
上的动点,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() .若已知
.若已知![]() ,设
,设![]() 两点间的距离为
两点间的距离为![]() 两点间的距离为
两点间的距离为![]() 两点间的距离为
两点间的距离为![]() .(若同学们打印的BC的长度如不是
.(若同学们打印的BC的长度如不是![]() ,请同学们重新画图、测量)
,请同学们重新画图、测量)
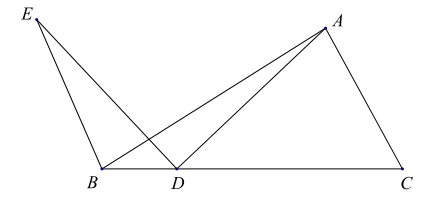
小明根据学习函数的经验,分别对![]() 自变量x的变化而变化的规律进行了探究,下面是小明的探究过程,请补充完整:
自变量x的变化而变化的规律进行了探究,下面是小明的探究过程,请补充完整:
(1)按照下表中自变量![]() 的值进行取点、画图、测量,分别得到了
的值进行取点、画图、测量,分别得到了![]() 与
与![]() 的几组对应值,如下表:
的几组对应值,如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 7.03 | 6.20 | 5.44 | 4.76 | 4.21 | 3.85 | 3.73 | 3.87 | 4.26 |
|
| 5.66 | 4.32 |
| 1.97 | 1.59 | 2.27 | 3.43 | 4.73 |
写出![]() 的值.(保留1位小数)
的值.(保留1位小数)
(2)在同一平面直角坐标系![]() 中,描出补全后的表中各组数值所对应的点
中,描出补全后的表中各组数值所对应的点![]() ,并画出函数
,并画出函数![]() 的图象;
的图象;
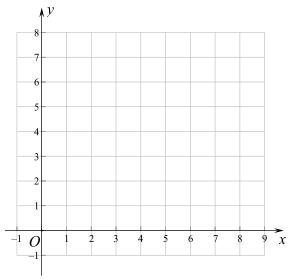
(3)结合函数图像,解决问题:
①当![]() 在线段
在线段![]() 上时,
上时,![]() 的长度约为________
的长度约为________![]() ;
;
②当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长度
的长度![]() 约为_______
约为_______![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七巧板是我国古老的益智玩具,受到全世界人的追捧.下图是由一副“现代智力七巧板经无缝拼接且没有重叠的轴对称花朵型图案,直线AB为对称轴,其中①②③是直径为1的圆与半圆,④为直角梯形,⑤为等腰直角三角形,⑥⑦是有一组对边平行且锐角皆为45°的拼板.若已知④的周长是AB的3倍,⑥的周长是AB的5倍,则图中线段AC的长度为_____.
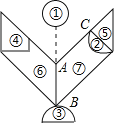
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+(3b+1)x+b﹣3(a>0),若存在实数m,使得点P(m,m)在该抛物线上,我们称点P(m,m)是这个抛物线上的一个“和谐点”.
(1)当a=2,b=1时,求该抛物线的“和谐点”;
(2)若对于任意实数b,抛物线上恒有两个不同的“和谐点”A、B.
①求实数a的取值范围;
②若点A,B关于直线y=﹣x﹣(![]() +1)对称,求实数b的最小值.
+1)对称,求实数b的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
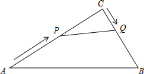
【题目】如图,已知△ABC,直线PQ垂直平分AC,与边AB交于E,连接CE,过点C作CF平行于BA交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
(3)若AD=3,AE=5,则菱形AECF的面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
(3)从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm,现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿CB向点B方向运动,如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动.设运动时间为t秒.求:
(1)当t=3秒时,这时,P,Q两点之间的距离是多少?
(2)若△CPQ的面积为S,求S关于t的函数关系式.
(3)当t为多少秒时,以点C,P,Q为顶点的三角形与△ABC相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 两点(点
两点(点![]() 位于点
位于点![]() 的左侧),与
的左侧),与![]() 轴相交于点
轴相交于点![]() ,
,![]() 是抛物线的顶点,直线
是抛物线的顶点,直线![]() 是抛物线的对称轴,且点
是抛物线的对称轴,且点![]() 的坐标为
的坐标为![]() .
.
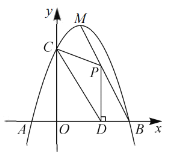
(1)求抛物线的解析式.
(2)已知![]() 为线段
为线段![]() 上一个动点,过点
上一个动点,过点![]() 作
作![]() 轴于点
轴于点![]() .若
.若![]() 的面积为
的面积为![]() .
.
①求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
②当![]() 取得最值时,求点
取得最值时,求点![]() 的坐标.
的坐标.
(3)在(2)的条件下,在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为等腰三角形?如果存在,请求出点
为等腰三角形?如果存在,请求出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
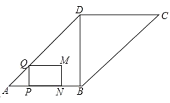
【题目】如图,在ABCD中,∠ABD=90°,AD= 5,BD=3,点P从点A出发,沿折线AB- BC以每秒个单位长度的速度向终点C运动(点P不与点A、B、C重合).在点P运动的过程中,过点P作AB所在直线的垂线.交边AD或边CD于点Q,以PQ为一边作矩形PQMN,且QM=2.MN与BD在PQ的同侧,设点P的运动时间为t(秒),
(1)当t= 5时,求线段CP的长;
(2)求线段PQ的长(用含t的代数式表示);
(3)当点M落在BD上时,求t的值;
(4)当矩形PQMN与ABCD重叠部分圆形为五边形时,直接写出t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com