
【题目】阅读下面材料:
小昊遇到这样一个问题:如图1,在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,求 ![]() 的值.
的值.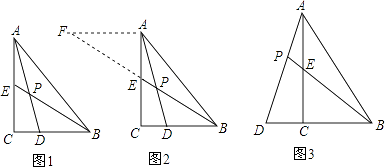
(1)小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).
请回答: ![]() 的值为 .
的值为 .
(2)参考小昊思考问题的方法,解决问题:
如图3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3.
①求 ![]() 的值;
的值;
(3)②若CD=2,则BP= .
【答案】
(1)![]()
(2)过点A作AF∥DB,交BE的延长线于点F,如图,
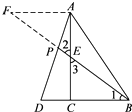
设DC=k,由DC:BC=1:2得BC=2k,DB=DC+BC=3k.
∵E是AC中点,
∴AE=CE.
∵AF∥DB,
∴∠F=∠1.
在△AEF和△CEB中,
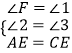 ,
,
∴△AEF≌△CEB,
∴EF=BE,AF=BC=2k.
∵AF∥DB,
∴△AFP∽△DBP,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() .
.
∴ ![]() 的值为
的值为 ![]()
(3)6
【解析】解:(1) ![]() 的值为
的值为 ![]() .
.
提示:易证△AEF≌△CEB,则有AF=BC.
设CD=k,则DB=2k,AF=BC=3k,
由AF∥BC可得△APF∽△DPB,
即可得到 ![]() =
= ![]() =
= ![]() .
.
所以答案是: ![]() ;
;
·(3)②当CD=2时,BC=4,AC=6,
∴EC= ![]() AC=3,EB=
AC=3,EB= ![]() =5,
=5,
∴EF=BE=5,BF=10.
∵ ![]() =
= ![]() (已证),
(已证),
∴ ![]() =
= ![]() ,
,
∴BP= ![]() BF=
BF= ![]() ×10=6.
×10=6.
所以答案是6.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a,b满足![]() +(c-7)2=0.
+(c-7)2=0.
(1) a= ,b= ,c= .
(2) 若将数轴折叠,使得A点与C点重合,则点B与数 表示的点重合.
(3) 点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB= ,AC= ,BC= .(用含t的代数式表示)
(4) 请问:3BC-2AB的值是否随着时间t的变化而改变? 若变化,请说明理由;若不变,请求其值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线;
②∠ADC=60°;
③点D在AB的中垂线上;
④BD=2CD.

A.4 B.3 C.2 D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠1=∠2,G为AD的中点,BG的延长线交AC于点E,F为AB上的一点,CF与AD垂直,交AD于点H,则下面判断正确的有( )

①AD是△ABE的角平分线;②BE是△ABD的边AD上的中线;
③CH是△ACD的边AD上的高;④AH是△ACF的角平分线和高
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,
(1)写出数轴上点B表示的数 ;
(2)|5﹣3|表示5与3之差的绝对值,实际上也可理解为5与3两数在数轴上所对的两点之间的距离.如|x﹣3|的几何意义是数轴上表示有理数x的点与表示有理数3的点之间的距离.试探索:
①:若|x﹣8|=2,则x= .
②:|x+12|+|x﹣8|的最小值为 .
(3)动点P从O点出发,以每秒5个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.求当t为多少秒时?A,P两点之间的距离为2;
(4)动点P,Q分别从O,B两点,同时出发,点P以每秒5个单位长度沿数轴向右匀速运动,Q点以P点速度的两倍,沿数轴向右匀速运动,设运动时间为t(t>0)秒.问当t为多少秒时?P,Q之间的距离为4.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC的边长为4cm,点P,Q分别从B,C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;
点Q沿CA,AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s),
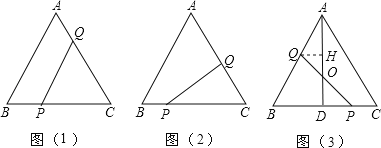
(1)如图(1),当x为何值时,PQ∥AB;
(2)如图(2),若PQ⊥AC,求x;
(3)如图(3),当点Q在AB上运动时,PQ与△ABC的高AD交于点O,OQ与OP是否总是相等?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:
(1) 5(x+8)=6(2x-7)+5;
(2) 5-![]() =x;
=x;
(3) ![]() -
-![]() =1;
=1;
(4) ![]() -
-![]() =1;
=1;
(5) 2x-![]() [x-
[x-![]() (x-1)]=
(x-1)]=![]() ( x-1).
( x-1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售“喜羊羊”玩具,预测该产品能够畅销,就用32000元购进了一批这种玩具,上市后很快脱销,商场又用68000元购进第二批这种玩具,所购数量是第一批购进数量的2倍,但每个进价多了10元.
(1)该商场两次共购进这种玩具多少个?
(2)如果这两批玩具每套的售价相同,且全部售完后总利润率不低于20%,那么每件售价至少是多少元?(利润率![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com