
分析 (1)先将减法转化为加法,再根据有理数加法法则计算即可;
(2)利用分配律计算即可;
(3)先算乘方与绝对值,再算乘除,最后算加减;
(4)先将除法转化为乘法,再根据有理数乘法法则计算即可.
解答 解:(1)$\frac{5}{13}$-(+3.7)+(+$\frac{8}{13}$)-(-1.7)
=$\frac{5}{13}$-3.7+$\frac{8}{13}$+1.7
=1-2=-1;
(2)($\frac{2}{3}$-$\frac{5}{6}$-$\frac{7}{8}$+$\frac{1}{12}$)×(-24)
=-16+20+21-2
=23;
(3)-32×(-2)+42÷(-2)3-|-22|
=-9×(-2)+16÷(-8)-4
=18-2-4
=12;
(4)-27÷2$\frac{1}{2}$×$\frac{4}{9}$
=-27×$\frac{2}{5}$×$\frac{4}{9}$
=-$\frac{24}{5}$.
点评 本题考查了有理数混合运算,顺序为:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.进行有理数的混合运算时,注意各个运算律的运用,使运算过程得到简化.


科目:初中数学 来源: 题型:解答题
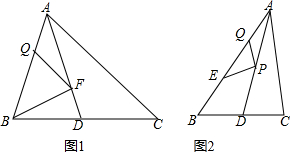
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
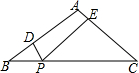 △ABC中,AB=AC=5,BC=8,点P是BC边上的动点,过点P作PD⊥AB于点D,PE⊥AC于点E,则PD+PE的长是( )
△ABC中,AB=AC=5,BC=8,点P是BC边上的动点,过点P作PD⊥AB于点D,PE⊥AC于点E,则PD+PE的长是( )| A. | 4.8 | B. | 4.8或3.8 | C. | 3.8 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
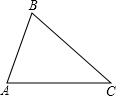 已知△ABC,请按以下要求完成本题:
已知△ABC,请按以下要求完成本题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com