练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
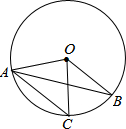
    4．如图，在⊙O中，弦AC与半径OB平行，若∠BOC=50°，则∠B的大小为（　　）
    A．25°B．30°C．50°D．60°

    分析 由弦AC与半径OB平行，若∠BOC=50°，可求得∠C的度数，继而求得∠AOC的度数，继而求得∠AOB的度数，然后由等腰三角形的性质，求得答案．

    解答 解：∵弦AC∥OB，∠BOC=50°，
    ∴∠C=∠BOC=50°，
    ∵OA=OC，
    ∴∠OAC=∠C=50°，
    ∴∠AOC=80°，
    ∴∠AOB=∠AOC+∠BOC=130°，
    ∵OA=OB，
    ∴∠B=∠OAB=25°．
    故选A．

    点评 此题考查了圆周角定理、平行线的性质以及等腰三角形的性质．注意求得∠AOB的度数是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    10．下列运算结果正确的是（　　）
    A．a+2b=3abB．3a2-2a2=1C．a2•a4=a8D．（-a2b）3÷（a3b）2=-b

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．2016年5月24日《天津日报》报道，2015年天津外环线内新栽植树木6120000株，将6120000用科学记数法表示应为（　　）
    A．0.612×107B．6.12×106C．61.2×105D．612×104

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．解不等式组$\left\{\begin{array}{l}{3x+1≤2（x+1）}\\{-x＜5x+12}\end{array}\right.$，并写出它的整数解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．小李用围棋子排成下列一组有规律的图案，其中第1个图案有1枚棋子，第2个图案有3枚棋子，第3个图案有4枚棋子，第4个图案有6枚棋子，…，那么第9个图案的棋子数是13枚．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．油电混动汽车是一种节油、环保的新技术汽车．它将行驶过程中部分原本被浪费的能量回收储存于内置的蓄电池中．汽车在低速行驶时，使用蓄电池带动电动机驱动汽车，节约燃油．某品牌油电混动汽车与普通汽车的相关成本数据估算如下：
     油电混动汽车普通汽车
    购买价格17.4815.98
    每百公里燃油成本（元）3146
    某人计划购入一辆上述品牌的汽车．他估算了未来10年的用车成本，在只考虑车价和燃油成本的情况下，发现选择油电混动汽车的成本不高于选择普通汽车的成本．则他在估算时，预计平均每年行驶的公里数至少为（　　）
    A．5 000B．10 000C．15 000D．20 000

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．如图，A，B，C是⊙O上三个点，∠ACB=30°，则∠BAO的度数是（　　）
    A．55°B．60°C．65°D．70°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

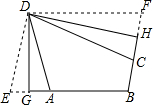    13．定义：有三个内角相等的四边形叫三等角四边形．
    （1）三等角四边形ABCD中，∠A=∠B=∠C，求∠A的取值范围；
    （2）如图，折叠平行四边形纸片DEBF，使顶点E，F分别落在边BE，BF上的点A，C处，折痕分别为DG，DH．求证：四边形ABCD是三等角四边形．
    （3）三等角四边形ABCD中，∠A=∠B=∠C，若CB=CD=4，则当AD的长为何值时，AB的长最大，其最大值是多少？并求此时对角线AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．根据国家发改委实施“阶梯水价”的有关文件要求，某市结合地方实际，决定从2016年1月1日起对居民生活用水按新的“阶梯水价”标准收费，某中学研究学习小组的同学们在社会实践活动中调查了30户家庭某月的用水量，如表所示：
    用水量（吨）1520253035
    户数36795
    则这30户家庭该用用水量的众数和中位数分别是（　　）
    A．25，27B．25，25C．30，27D．30，25

    查看答案和解析>>

    同步练习册答案