
 附加题:
附加题: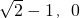 ),B(
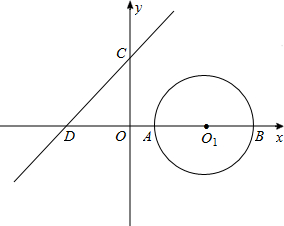
),B(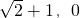 ).直线y=x+1与坐标轴交于C、D两点,直线在⊙O1的左侧.
).直线y=x+1与坐标轴交于C、D两点,直线在⊙O1的左侧. 解:(1)如图.
解:(1)如图. ×OC×OD=
×OC×OD= ×1×1=
×1×1= ;
; AB=1.
AB=1. 将O1点的坐标(
将O1点的坐标( ,0)代入,
,0)代入, +t=0,解得t=
+t=0,解得t= ,
, .
. ,得
,得 ,
, ,
, ).
). -
- )2+(
)2+( )2=1,
)2=1, (不合题意,舍去).
(不合题意,舍去). ,0)代入,运用待定系数法求出直线O1M的解析式,将它与所求直线l的解析式y=x+b联立,得出用含b的代数式表示两直线的交点M的坐标,然后根据O1M=1列出关于b的方程,解方程即可.
,0)代入,运用待定系数法求出直线O1M的解析式,将它与所求直线l的解析式y=x+b联立,得出用含b的代数式表示两直线的交点M的坐标,然后根据O1M=1列出关于b的方程,解方程即可.

 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
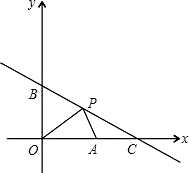 附加题:如图,在平面直角坐标系中,A点的坐标为(4,0),点P是直线y=-
附加题:如图,在平面直角坐标系中,A点的坐标为(4,0),点P是直线y=-| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 附加题:
附加题:| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:2011-2012学年广西南宁九中九年级(上)期中数学试卷(解析版) 题型:解答题
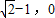 ),B(
),B(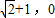 ).直线y=x+1与坐标轴交于C、D两点,直线在⊙O1的左侧.
).直线y=x+1与坐标轴交于C、D两点,直线在⊙O1的左侧.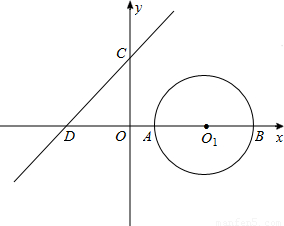
查看答案和解析>>
科目:初中数学 来源:浙江省期末题 题型:解答题
 ,消去y化简得:2x2-7x+6=0,
,消去y化简得:2x2-7x+6=0,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com