
【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径作⊙O,点D为⊙O上一点,且CD=CB、连接DO并延长交CB的延长线于点E.
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)若BE=4,DE=8,求AC的长.

【答案】(1)相切,证明见解析;(2)6![]() .
.
【解析】
(1)欲证明CD是切线,只要证明OD⊥CD,利用全等三角形的性质即可证明;
(2)设⊙O的半径为r.在Rt△OBE中,根据OE2=EB2+OB2,可得(8﹣r)2=r2+42,推出r=3,由tan∠E=![]() ,推出
,推出![]() ,可得CD=BC=6,再利用勾股定理即可解决问题.
,可得CD=BC=6,再利用勾股定理即可解决问题.
(1)相切,理由如下,
如图,连接OC,
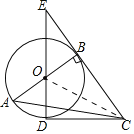
∵CB=CD,CO=CO,OB=OD,
∴△OCB≌△OCD,
∴∠ODC=∠OBC=90°,
∴OD⊥DC,
∴DC是⊙O的切线;
(2)设⊙O的半径为r,
在Rt△OBE中,∵OE2=EB2+OB2,
∴(8﹣r)2=r2+42,
∴r=3,AB=2r=6,
∵tan∠E=![]() ,
,
∴![]() ,
,
∴CD=BC=6,
在Rt△ABC中,AC=![]() .
.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(―3,6)、B(―9,一3),以原点O为位似中心,相似比为![]() ,把△ABO缩小,则点A的对应点A′的坐标是( )
,把△ABO缩小,则点A的对应点A′的坐标是( )

A.(―1,2)
B.(―9,18)
C.(―9,18)或(9,―18)
D.(―1,2)或(1,―2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:如图![]() ,在四边形
,在四边形![]() 的边
的边![]() 上任取一点
上任取一点![]() (点
(点![]() 不与
不与![]() 、
、![]() 重合),分别连接
重合),分别连接![]() 、
、![]() ,可以把四边形
,可以把四边形![]() 分成三个三角形,如果其中有两个三角形相似,我们就把
分成三个三角形,如果其中有两个三角形相似,我们就把![]() 叫做四边形
叫做四边形![]() 的边
的边![]() 上的“相似点”:如果这三个三角形都相似,我们就把
上的“相似点”:如果这三个三角形都相似,我们就把![]() 叫做四边形
叫做四边形![]() 的边
的边![]() 上的“强相似点”.解决问题:
上的“强相似点”.解决问题:
![]() 如图
如图![]() ,
,![]() ,试判断点
,试判断点![]() 是否是四边形
是否是四边形![]() 的边
的边![]() 上的相似点,并说明理由;
上的相似点,并说明理由;
![]() 如图
如图![]() ,在矩形
,在矩形![]() 中,
中,![]() 、
、![]() 、
、![]() 、
、![]() 四点均在正方形网格(网格中每个小正方形的边长为
四点均在正方形网格(网格中每个小正方形的边长为![]() )的格点(即每个小正方形的顶点)上,试在图②中画出矩形
)的格点(即每个小正方形的顶点)上,试在图②中画出矩形![]() 的边
的边![]() 上的强相似点;
上的强相似点;
![]() 如图
如图![]() ,将矩形
,将矩形![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在
落在![]() 边上的点
边上的点![]() 处,若点
处,若点![]() 恰好是四边形
恰好是四边形![]() 的边
的边![]() 上的一个强相似点,试探究
上的一个强相似点,试探究![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,先描出点![]() ,点
,点![]() .
.

(1)描出点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 的位置,写出
的位置,写出![]() 的坐标 ;
的坐标 ;
(2)用尺规在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小(保留作图痕迹);
的值最小(保留作图痕迹);
(3)用尺规在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() (保留作图痕迹).
(保留作图痕迹).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若PD=![]() ,求⊙O的直径.
,求⊙O的直径.

查看答案和解析>>
科目:初中数学 来源: 题型:
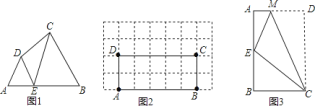
【题目】在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线, DE⊥AB于点E.

(1)如图1,连接EC,求证:△EBC是等边三角形;
(2)点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G.请你在图2中画出完整图形,并直接写出MD,DG与AD之间的数量关系;
(3)如图3,点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G,且MB=MG.试探究ND,DG与AD数量之间的关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是菱形
是菱形![]() 的对角线
的对角线![]() 、
、![]() 的交点,
的交点,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.下列结论:①
的中点.下列结论:①![]() ;②四边形
;②四边形![]() 也是菱形;③四边形
也是菱形;③四边形![]() 的面积为
的面积为![]() ;④
;④![]() ;⑤
;⑤![]() 是轴对称图形.其中正确的结论有( )
是轴对称图形.其中正确的结论有( )
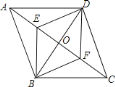
A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com