
【题目】如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF.给出下列条件:
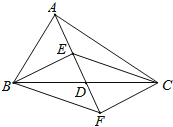
①BE⊥EC;②BF∥CE;③AB=AC;
从中选择一个条件使四边形BECF是菱形,你认为这个条件是 (只填写序号).
科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数y= ![]() 的图象上,过点A,B作x轴的垂线,垂足分别是M,N,射线AB交x轴于点C,若OM=MN=NC,四边形AMNB的面积是3,则k的值为( )
的图象上,过点A,B作x轴的垂线,垂足分别是M,N,射线AB交x轴于点C,若OM=MN=NC,四边形AMNB的面积是3,则k的值为( ) 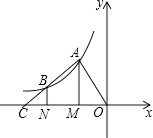
A.2
B.4
C.﹣2
D.﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校20周年校庆时,需要在草场上利用气球悬挂宣传条幅,EF为旗杆,气球从A处起飞,几分钟后便飞达C处,此时,在AF延长线上的点B处测得气球和旗杆EF的顶点E在同一直线上.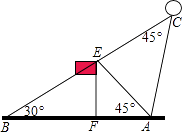
(1)已知旗杆高为12米,若在点B处测得旗杆顶点E的仰角为30°,A处测得点E的仰角为45°,试求AB的长(结果保留根号);
(2)在(1)的条件下,若∠BCA=45°,绳子在空中视为一条线段,试求绳子AC的长(结果保留根号)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线相交于点O,过点D作DE∥AC,且DE= ![]() AC,连接CE,OE,连接AE,交OD于点F.若AB=2,∠ABC=60°,则AE的长为( )
AC,连接CE,OE,连接AE,交OD于点F.若AB=2,∠ABC=60°,则AE的长为( ) 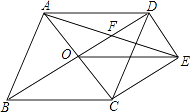
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
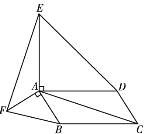
【题目】如图,在□ABCD的形外分别作等腰直角△ABF和等腰直角△ADE,∠FAB=∠EAD=90°,
连结AC、EF.在图中找一个与△FAE全等的三角形,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长交AD于E,交BA的延长线于点F.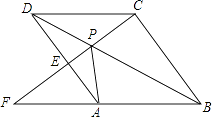
(1)求证:△APD≌△CPD;
(2)求证:△APE∽△FPA;
(3)猜想:线段PC,PE,PF之间存在什么关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区准备新建50个停车位,用以解决小区停车难的问题.已知新建1个地上停车位和1个地下停车位共需0.6万元;新建3个地上停车位和2个地下停车位共需1.3万元.
(1)该小区新建1个地上停车位和1个地下停车位各需多少万元?
(2)该小区的物业部门预计投资金额超过12万元而不超过13万元,那么共有几种建造停车位的方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,P,Q分别是BC,AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R,S,若AQ=PQ,PR=PS,则这四个结论中正确的有( )
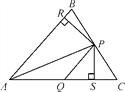
①PA平分∠BAC;②AS=AR;③QP∥AR;④△BRP≌△CSP.
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
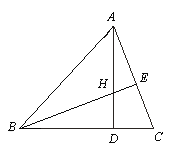
【题目】(8分)如图,△ABC的两条高AD、BE相交于点H,且AD=BD,试说明下列结论成立的理由。(1)∠DBH=∠DAC;(2)△BDH≌△ADC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com