
分析 根据题意可以求得变化前与变化后梯形的面积,从而可以解答本题.
解答 解:一个梯形上底长acm,下底长bcm,高为ccm的面积是:$\frac{(a+b)c}{2}$,
变化后的梯形的面积是:$\frac{(\frac{1}{2}a+2b)c}{2}$,
∴梯形面积增加了:$\frac{(\frac{1}{2}a+2b)c}{2}-\frac{(a+b)c}{2}$=$\frac{(-\frac{1}{2}a+b)c}{2}$=$\frac{1}{4}(2b-a)c$=$\frac{bc}{2}-\frac{ac}{4}$,
即梯形的面积增加($\frac{bc}{2}-\frac{ac}{4}$)cm2.
点评 本题考查整式的混合运算,解题的关键是明确整式的混合运算的计算方法.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
 如图,点M是边长为4cm的正方形的边AB的中点,点P是正方形边上的动点,从点M出发沿着逆时针方向在正方形的边上以每秒1cm的速度运动,则当点P逆时针旋转一周时,随着运动时间的增加,△DMP面积达到5cm2的时刻的个数是( )
如图,点M是边长为4cm的正方形的边AB的中点,点P是正方形边上的动点,从点M出发沿着逆时针方向在正方形的边上以每秒1cm的速度运动,则当点P逆时针旋转一周时,随着运动时间的增加,△DMP面积达到5cm2的时刻的个数是( )| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=6,请你在直线BC上找出一点P,使得△PAB为等腰三角形.要求:
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=6,请你在直线BC上找出一点P,使得△PAB为等腰三角形.要求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
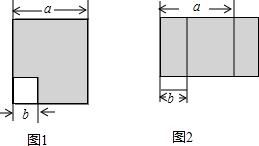
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AD∥BC,AB⊥BC,对角线AC⊥CD,点E在边BC上,且∠AEB=45°,CD=10.
如图,在四边形ABCD中,AD∥BC,AB⊥BC,对角线AC⊥CD,点E在边BC上,且∠AEB=45°,CD=10.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com