
| 1 |
| 2 |
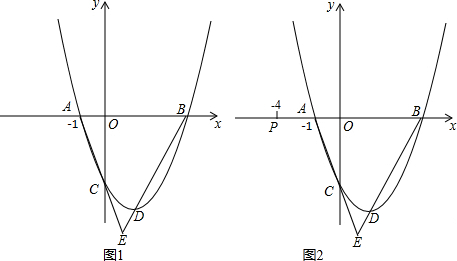
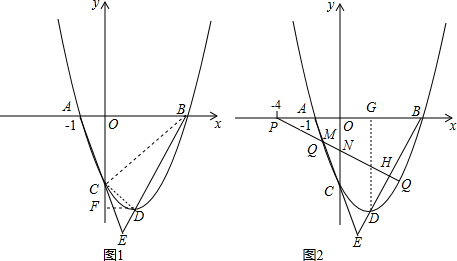 解:(1)把x=-1,y=0代入y=x2-2x+c得:1+2+c=0
解:(1)把x=-1,y=0代入y=x2-2x+c得:1+2+c=0| 2 |
| 2 |
| CD |
| CB |
| OA |
| OC |
| BG |
| DG |
| ON |
| OP |
| 2 |
| 4 |
| ON |
| 4 |
|
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 4 |
| 1 |
| 2 |
| 7 |
| 4 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
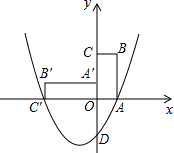 (2013•十堰模拟)如图,矩形OABC绕点O逆时针旋转90°得,矩形OA′B′C′,已知OA=1,AB=3,抛物线y=x2+bx+c过点A,C′,与y轴相交于点D.
(2013•十堰模拟)如图,矩形OABC绕点O逆时针旋转90°得,矩形OA′B′C′,已知OA=1,AB=3,抛物线y=x2+bx+c过点A,C′,与y轴相交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•十堰)张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.以下说法错误的是( )
(2013•十堰)张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.以下说法错误的是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com