
【题目】材料:在学习绝对值时,老师教过我们绝对值的几何含义,![]() 表示
表示![]() 、
、![]() 在数轴上对应的两点之间的距离;
在数轴上对应的两点之间的距离;![]() ,所以
,所以![]() 表示
表示![]() 、
、![]() 在数轴上对应的两点之间的距离;
在数轴上对应的两点之间的距离;![]() ,所以
,所以![]() 表示
表示![]() 在数轴上对应的点到原点的距离,一般地,点
在数轴上对应的点到原点的距离,一般地,点![]() 、
、![]() 在数轴上分别表示有理数
在数轴上分别表示有理数![]() 、
、![]() ,那么
,那么![]() 、
、![]() 之间的距离可表示为
之间的距离可表示为![]() .
.
(![]() )点
)点![]() 、
、![]() 、
、![]() 在数轴上分别表示有理数
在数轴上分别表示有理数![]() 、
、![]() 、
、![]() ,那么
,那么![]() 到
到![]() 的距离表示为______________________________(用含绝对值的式子表示).如果
的距离表示为______________________________(用含绝对值的式子表示).如果![]() ,那么
,那么![]() 为______________________________.
为______________________________.
(![]() )利用数轴探究:
)利用数轴探究:
①找出满足![]() 的
的![]() 的所有整数值是____________________;
的所有整数值是____________________;
②设![]() ,当
,当![]() 的值取在不小于
的值取在不小于![]() 且不大于
且不大于![]() 的范围时,
的范围时,![]() 的值是不变的,而且是
的值是不变的,而且是![]() 的最小值,这个最小值是____________________;
的最小值,这个最小值是____________________;
(![]() )求
)求![]() 的最小值为____________________,此时
的最小值为____________________,此时![]() 的值为____________________.
的值为____________________.
【答案】(1)|x+2|,-4或0;(2)①-2,4;②2;(3)4,2
【解析】
(1)根据两点间的距离公式,可得答案;
(2)①根据两点间的距离公式,分三种情况分析;
②根据当x的值取在不小于1且不大于3的范围时有最小值,化简即可求出p的值;
(3) |x-3|+|x-2|+|x+1|=(|x-3|+|x+1|)+|x-2|,根据问题(2)中的②可知,要使|x-3|+|x+1|的值最小,x的值只要取-1到3之间(包括-1、3)的任意一个数,要使|x-2|的值最小,x应取2,显然当x=2时能同时满足要求,把x=2代入原式计算即可;
(1)A到B的距离表示为:|x-(-2)|=|x+2|,
|AB|=2即|x+2|=2,∴x=-4或x=0.
(2)①根据绝对值的几何含义可得,|x-3|+|x+1|表示数轴上x与3的距离与x与-1的距离之和,
若x<-1,则3-x+(-x-1)=6,即x=-2;
若-1≤x≤3,则3-x+x+1=6,方程无解,舍去;
若x>3,则x-3+x+1=6,即x=4,
∴满足|x-3|+|x+1|=6的x的所有值是-2,4;
②当x的值取在不小于1且不大于3的范围时,p的值是不变的,而且是p的最小值.
|x3|+|x+1|=3-x+x+3=4,
即p=4,则这个最小值是4;
(3)|x-3|+|x-2|+|x+1|=(|x-3|+|x+1|)+|x-2|,根据问题(2)中的②可知,要使|x-3|+|x+1|的值最小,x的值只要取-1到3之间(包括-1、3)的任意一个数,要使|x-2|的值最小,x应取2,当x=2时能同时满足要求,把x=2代入,原式=1+0+3=4.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】如图1,一副直角三角板![]() 和
和![]() ,
,![]() ,将
,将![]() 和
和![]() 放置如图2的位置,点
放置如图2的位置,点![]() 、
、![]() 、
、![]() 、
、![]() 在同一直线上。
在同一直线上。

(1)如图3,![]() 固定不动,
固定不动,![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 时,判断
时,判断![]() 与
与![]() 的位置关系,并说明理由。
的位置关系,并说明理由。
(2)在图2的位置上,![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,在旋转过程中,两个三角形的边是否存在垂直关系?若存在直接写出旋转的角度,并写出哪两边垂直,若不存在,请说明理由。
,在旋转过程中,两个三角形的边是否存在垂直关系?若存在直接写出旋转的角度,并写出哪两边垂直,若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形![]() 中,
中,![]() ,
,![]() ,动点
,动点![]() 从
从![]() 出发,以每秒1个单位的速度沿射线
出发,以每秒1个单位的速度沿射线![]() 方向移动,作
方向移动,作![]() 关于直线
关于直线![]() 的对称
的对称![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() .
.


(1)当![]() 时.
时.
①如图2.当点![]() 落在
落在![]() 上时,显然
上时,显然![]() 是直角三角形,求此时
是直角三角形,求此时![]() 的值;
的值;
②当点![]() 不落在
不落在![]() 上时,请直接写出
上时,请直接写出![]() 是直角三角形时
是直角三角形时![]() 的值;
的值;
(2)若直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,且当
,且当![]() 时,
时,![]() .问:当
.问:当![]() ,
,![]() 的大小是否发生变化,若不变,请说明理由.
的大小是否发生变化,若不变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张扑克牌(方块2、黑桃4、黑桃5、梅花5)的牌面如图l,将扑克牌洗匀后,如图2背面朝上放置在桌面上.小亮和小明设计的游戏规则是两人同时抽取一张扑克牌,两张牌面数字之和为奇数时,小亮获胜;否则小明获胜.请问这个游戏规则公平吗?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小王某天下午营运是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天下午行车里程(单位:千米)如下:
+15,-2,+5,-1,+10,-3,-2,+12,+4,-5,+6.
(1)将最后一名乘客送到目的地时,小王距下午出车时的出发点多远?
(2)若汽车耗油量为0.05升/千米,这天下午小王的汽车共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A、B、C分别在l1、l2、l3上,AC交l2于D,∠ACB=90°.已知l1与l2的距离为2,l2与l3的距离为6,则![]() 的值为_____.
的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图E、F分别在正方形ABCD的边BC、CD上,且∠EAF=45°.
(1)求证:EF=BE+DF;
(2)若线段EF、AB的长分别是方程x2﹣5x+6=0的两个根,求△AEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
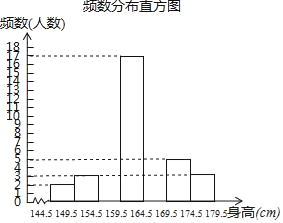
【题目】为了解同学们的身体发育情况,学校体卫办公室对七年级全体学生进行了身高测量(精确到1cm),并从中抽取了部分数据进行统计,请根据尚未完成的频数分布表和频数分布直方图解答下列问题:
频率分布表
分组 | 频数 | 百分比 |
144.5~149.5 | 2 | 4% |
149.5~154.5 | 3 | 6% |
154.5~159.5 | a | 16% |
159.5~164.5 | 17 | 34% |
164.5~169.5 | b | n% |
169.5~174.5 | 5 | 10% |
174.5~179.5 | 3 | 6% |
(1)求a、b、n的值;
(2)补全频数分布直方图;
(3)学校准备从七年级学生中选拔护旗手,要求身高不低于170cm,如果七年级有学生350人,护旗手的候选人大概有多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com