
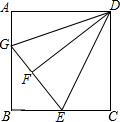
 如图,正方形ABCD,AB=10,E为BC的中点,将正方形的边CD沿着DE折叠到DF,延长EF交AB于G,连接DG.
如图,正方形ABCD,AB=10,E为BC的中点,将正方形的边CD沿着DE折叠到DF,延长EF交AB于G,连接DG.分析 (1)欲证明△ADG≌△FDG只要证明AD=DF,∠A=∠DFG=90°即可.
(2)设AG=GF=x,在RT△BEG中,由BG2+BE2=GE2列出方程即可求出x,再根据三角形面积公式计算即可.
解答 (1)证明:∵四边形ABCD是正方形,
∴DC=AD,∠C=∠A=90°,
∵△DEF是由△DEC翻折得到,
∴DF=DC,∠DFE=∠DFG=∠C=90°,
∴∠A=∠DFG,AD=DF,
在RT△DGA和RT△DGF中,
$\left\{\begin{array}{l}{DG=DG}\\{DA=DF}\end{array}\right.$,
∴△DGA≌△DGF.
(2)解:∵△DGA≌△DGF,
∴AG=GF,设AG=GF=x,
∵BE=EC=EF=5,
在RT△BEG中,
∵BG2+BE2=GE2,
∴(10-x)2+52=(x+5)2,
∴x=$\frac{10}{3}$,
∴BG=AB-AG=10-$\frac{10}{3}$=$\frac{20}{3}$
∴S△BEG=$\frac{1}{2}$×5×$\frac{20}{3}$=$\frac{50}{3}$.
点评 本题考查正方形的性质、全等三角形的判定和性质、翻折变换等知识,解题的关键是熟练掌握全等三角形的判定和性质,学会用方程的思想思考问题,属于中考常考题型.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 所示的不完整统计表和扇形统计图:
所示的不完整统计表和扇形统计图:| 八年级2班参加球类活动人数统计表 | |||||
| 项目 | 篮球 | 足球 | 乒乓球 | 排球 | 羽毛球 |
| 人数 | a | 6 | 5 | 7 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com