
分析 把P点代入y=$\frac{2}{x}$求得P的坐标,进而求得OP的长,即可求得Q的坐标,从而求得k的值.
解答 解:∵点P(1,t)在反比例函数y=$\frac{2}{x}$的图象上,
∴t=$\frac{2}{1}$=2,
∴P(1.2),
∴OP=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∵过点P作直线l与x轴平行,点Q在直线l上,满足QP=OP.
∴Q(1+$\sqrt{5}$,2)或(1-$\sqrt{5}$,2)
∵反比例函数y=$\frac{k}{x}$的图象经过点Q,
∴2=$\frac{k}{1+\sqrt{5}}$或2=$\frac{k}{1-\sqrt{5}}$,解得k=2+2$\sqrt{5}$或2-2$\sqrt{5}$
故答案为2+2$\sqrt{5}$或2-2$\sqrt{5}$.
点评 本题考查了反比例函数图象上点的坐标特征,勾股定理的应用,求得Q点的坐标是解题的关键.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:解答题
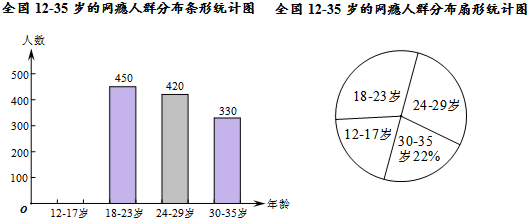
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,把一个小球垂直向上抛出,则下列描述该小球的运动速度v(单位:m/s)与运动时间t(单位s)关系的函数图象中,正确的是( )
如图,把一个小球垂直向上抛出,则下列描述该小球的运动速度v(单位:m/s)与运动时间t(单位s)关系的函数图象中,正确的是( )| A. | 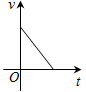 | B. | 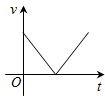 | C. | 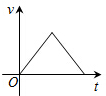 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.3×106 | B. | 3×105 | C. | 3×106 | D. | 30×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2+x4=x6 | B. | x6÷x3=x2 | ||
| C. | $\frac{-a-b}{a+b}$=-1 | D. | $\frac{b}{{a}^{2}-{b}^{2}}$÷(1-$\frac{a}{a+b}$)=-$\frac{1}{a-b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC=200m,∠CAB=54°,∠CBA=30°.
为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC=200m,∠CAB=54°,∠CBA=30°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{500}{x+30}=\frac{350}{x}$ | B. | $\frac{500}{x-30}=\frac{350}{x}$ | C. | $\frac{500}{x}=\frac{350}{x-30}$ | D. | $\frac{500}{x}=\frac{350}{x+30}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com