
【题目】如图,平行四边形ABCD的对角线AC,BD相交于点O,CE平分![]() 交BD于点F,且
交BD于点F,且![]() ,
,![]() ,连接OE,下列结论:①
,连接OE,下列结论:①![]() ;②
;②![]() ;③
;③![]() .其中正确的有( )
.其中正确的有( )
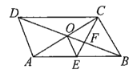
A.0个B.1个C.2个D.3个
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() ,点
,点![]() ,点
,点![]() .
.
(1)画出![]() 关于
关于![]() 轴的对称图形
轴的对称图形![]() ,并写出点
,并写出点![]() 的对称点
的对称点![]() 的坐标;
的坐标;
(2)若点![]() 在
在![]() 轴上,连接
轴上,连接![]() 、
、![]() ,则
,则![]() 的最小值是 ;
的最小值是 ;
(3)若直线![]() 轴,与线段
轴,与线段![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() (点
(点![]() 不与点
不与点![]() 重合),若将
重合),若将![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 的对称点为点
的对称点为点![]() ,当点
,当点![]() 落在
落在![]() 的内部(包含边界)时,点
的内部(包含边界)时,点 的横坐标
的横坐标![]() 的取值范围是 .
的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
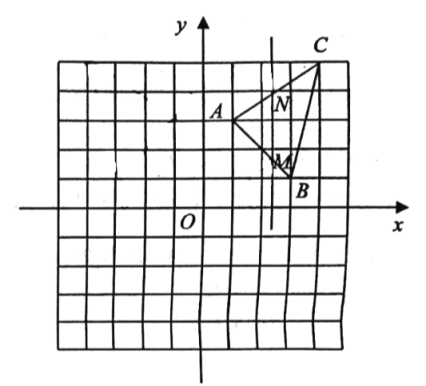
【题目】如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2,与y轴交于点C(0,﹣4),其中x1,x2是方程x2﹣4x﹣12=0的两个根.
(1)求A、B两点坐标;
(2)求抛物线的解析式;
(3)点M是线段AB上的一个动点(不与A、B两点重合),过点M作MN∥BC,交AC于点N,连接CM,在M点运动时,△CMN的面积是否存在最大值?若存在,求出△CMN面积最大时点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线![]() 、
、![]() 交于点
交于点![]() ,顺次联结ABCD各边中点得到的一个新的四边形,如果添加下列四个条件中的一个条件:①
,顺次联结ABCD各边中点得到的一个新的四边形,如果添加下列四个条件中的一个条件:①![]() ⊥
⊥![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,可以使这个新的四边形成为矩形,那么这样的条件个数是()
,可以使这个新的四边形成为矩形,那么这样的条件个数是()

A. 1个;B. 2个;
C. 3个;D. 4个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知二次函数y=mx2+3mx﹣![]() m的图象与x轴交于A,B两点(点A在点B的左侧),顶点D和点B关于过点A的直线l:y=﹣
m的图象与x轴交于A,B两点(点A在点B的左侧),顶点D和点B关于过点A的直线l:y=﹣![]() x﹣
x﹣![]() 对称.
对称.
(1)求A、B两点的坐标及二次函数解析式;
(2)如图2,作直线AD,过点B作AD的平行线交直线1于点E,若点P是直线AD上的一动点,点Q是直线AE上的一动点.连接DQ、QP、PE,试求DQ+QP+PE的最小值;若不存在,请说明理由:
(3)将二次函数图象向右平移![]() 个单位,再向上平移3
个单位,再向上平移3![]() 个单位,平移后的二次函数图象上存在一点M,其横坐标为3,在y轴上是否存在点F,使得∠MAF=45°?若存在,请求出点F坐标;若不存在,请说明理由.
个单位,平移后的二次函数图象上存在一点M,其横坐标为3,在y轴上是否存在点F,使得∠MAF=45°?若存在,请求出点F坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯运营商的手机上网流量资费标准推出了三种优惠方案:
方案A:按流量计费,0.1元/M;
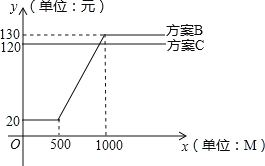
方案B:20元流量套餐包月,包含500M流量,如果超过500M,超过部分另外计费(见图象),如果用到1000M时,超过1000M的流量不再收费;
方案C:120元包月,无限制使用.
用x表示每月上网流量(单位:M),y表示每月的流量费用(单位:元),方案B和方案C对应的y关于x的函数图象如图所示,请解决以下问题:
(1)写出方案A的函数解析式,并在图中画出其图象;
(2)直接写出方案B的函数解析式;
(3)若甲乙两人每月使用流量分别在300—600M,800—1200M之间,请你分别给出甲乙二人经济合理的选择方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
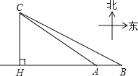
【题目】如图,在一笔直的海岸线上有![]() 、
、![]() 两个观测站,
两个观测站,![]() 在
在![]() 的正东方向,
的正东方向,![]() 千米,在某一时刻,从观测站
千米,在某一时刻,从观测站![]() 测得一艘集装箱货船位于北偏西
测得一艘集装箱货船位于北偏西![]() 的
的![]() 处,同时观测站
处,同时观测站![]() 测得改集装箱船位于北偏西
测得改集装箱船位于北偏西![]() 方向,问此时该集装箱船与海岸之间距离
方向,问此时该集装箱船与海岸之间距离![]() 约多少千米?(最后结果保留整数)
约多少千米?(最后结果保留整数)
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() ,
,![]() 为直线
为直线![]() 上两点,
上两点,![]() 为直线
为直线![]() 上两点.
上两点.
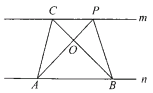
(1)如果固定点![]() ,点
,点![]() 在直线
在直线![]() 上移动,那么不论点
上移动,那么不论点![]() 移动到何处,总有
移动到何处,总有![]() _____与
_____与![]() 的面积相等,理由是_________________.
的面积相等,理由是_________________.
(2)如果![]() 处在如图所示位置,请写出另外两对面积相等的三角形:①_________________;②_________________.
处在如图所示位置,请写出另外两对面积相等的三角形:①_________________;②_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
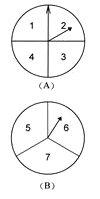
【题目】甲乙两人在玩转盘游戏时,把转盘A、B分别分成4等份、3等份,并在每一份内标上数字,如图所示.游戏规定,转动两个转盘停止后,指针所指的两个数字之和为奇数时,甲获胜;为偶数时,乙获胜.
(1)用列表法(或画树状图)求甲获胜的概率;
(2)你认为这个游戏规则对双方公平吗?请简要说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com