
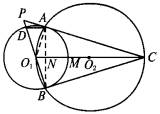
(1)求证:AC是⊙O1的切线;
(2)连结AD、O1C,求证:AD∥O1C;
(3)如果PD=1,⊙O1的半径为2,求BC的长
| (1)证明:连结O1 A.
∵ BC切⊙O1于B,∴ O1B⊥BC. ∴ O1C是⊙O2的直径.∴ O1A⊥AC.∴ AC是⊙O1的切线. (2)证法一:连结AB交O1C于N,O1C与⊙O1的弧 ∴ 证法二:∵ O1O2平分AB,O1D=O1B, ∴ O1N∥AD.即AD∥O1C. 证法三:∵ BD是⊙O1的直径, ∴ ∠DAB=90°.即AB⊥AD. 又∵ AB⊥O1C,∴ AD∥O1C. (3)解:∵ AD∥O1C,PD=1,O1D=2,∴ 设PA=x,则AC=2x. ∵ PA·PC=PD·PB,∴ x·3x=1×5. ∴ x= ∵ O1C垂直平分AB,∴ BC=AC=
|
| (1)要证AC是⊙O1的切线,只需连结O1A证明O1A⊥AC,则只需证O1C是直径,由BC是⊙O1的切线.可知O1B⊥BC.
故结论得证. (2)要证AD∥O1C,途径较多,①可证∠ADB=∠CO1B,观察到∠ADB是圆周角.所对的弧是 ②连结AB.可证AB⊥AD,AB⊥O1C.得AD∥O1C. ③连结AB交O1C于N,证明O1N是△ABD的中位线.亦可说明AD∥O1C. (3)由题意知已知量与BC无直接关系,而观察到BC与AC相等,AC是直线PC被平行线截得的部分,同时,AC还是割线PC的一部分,从这两个方面可得关于AC的方程.若设AC=x,可得PA= 又PD·PB=PA·PC,可求得AC.
|


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 24、如图,已知⊙O1与⊙O2相交于A、B两点,连心线O1O2交⊙O1于C、D两点,直线CA交⊙O2于点P,直线PD交⊙O1于点Q,且CP∥QB,求证:AC=AP.
24、如图,已知⊙O1与⊙O2相交于A、B两点,连心线O1O2交⊙O1于C、D两点,直线CA交⊙O2于点P,直线PD交⊙O1于点Q,且CP∥QB,求证:AC=AP.查看答案和解析>>
科目:初中数学 来源: 题型:
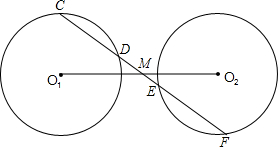 助线或另添字母),则M是线段O1O2的中点,并说明理由.(说明理由时可添加辅助线或字母)
助线或另添字母),则M是线段O1O2的中点,并说明理由.(说明理由时可添加辅助线或字母)查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知⊙O1与⊙O2相交于A、B两点,过A作⊙O1的切线交⊙O2于E,连接EB并延长交⊙O1于C,直线CA交⊙O2于点D.
如图,已知⊙O1与⊙O2相交于A、B两点,过A作⊙O1的切线交⊙O2于E,连接EB并延长交⊙O1于C,直线CA交⊙O2于点D.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知⊙O1与⊙O2的半径分别为r1,r2,⊙O2经过⊙O1的圆心O1,且两圆相交于A,B两点,C为⊙O2上的点,连接AC交⊙O1于D点,再连接BC,BD,AO1,AO2,O1O2,有如下四个结论:①∠BDC=∠AO1O2;②
如图,已知⊙O1与⊙O2的半径分别为r1,r2,⊙O2经过⊙O1的圆心O1,且两圆相交于A,B两点,C为⊙O2上的点,连接AC交⊙O1于D点,再连接BC,BD,AO1,AO2,O1O2,有如下四个结论:①∠BDC=∠AO1O2;②| BD |
| BC |
| r1 |
| r2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com