
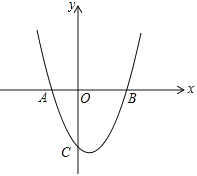
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪������![]() ��x�ύ��A����1��0����B��2��0�����㣬��y�ύ�ڵ�C��
��x�ύ��A����1��0����B��2��0�����㣬��y�ύ�ڵ�C��
��1����������ߵĽ���ʽ��
��2��ֱ��y=��x+n����������ڵ��������ڽ��ڵ�D�����߶�BC���ڵ�E����x�ύ�ڵ�F����BE=4EC��
����n��ֵ��
������AC��CD���߶�AC���߶�DF���ڵ�G����AGF����CGD�Ƿ�ȫ�ȣ���˵�����ɣ�
��3��ֱ��y=m��m��0����������ߵĽ���ΪM��N����M�ڵ�N����ࣩ���� M����y��ĶԳƵ�Ϊ��M'����H������Ϊ��1��0�������ı���OM'NH�����Ϊ![]() �����H��OM'�ľ���d��ֵ��
�����H��OM'�ľ���d��ֵ��
���𰸡���1��![]() ����2����n=��2���ڡ�AGF����CGDȫ������3��
����2����n=��2���ڡ�AGF����CGDȫ������3��![]() ��
��
��������
�����������1������������![]() ��x�ύ��A����1��0����B��2��0�����㣬�ɵ������ߵĽ���ʽ��
��x�ύ��A����1��0����B��2��0�����㣬�ɵ������ߵĽ���ʽ��
��2��������E��EE'��x����E'����EE'��OC������ƽ���߷��߶γɱ����������ɵ�BE'=4OE'�����E������Ϊ��x��y������OE'=x��BE'=4x������OB=2���ɵ�x��ֵ���ٸ���ֱ��BC�Ľ���ʽ���ɵõ�E����������E���������ֱ��y=��x+n���ɵ�n��ֵ��
������F����2��0����A����1��0�����ɵ�AF=1���ٸ��ݵ�D������Ϊ��1����3������C������Ϊ��0����3�����ɵ�CD��x�ᣬCD=1���ٸ�����AFG=��CDG����FAG=��DCG�������ж���AGF�ա�CGD��
��3��������ԳƵ����ʵó�OH=1=M'N�������ж��ı���OM'NH��ƽ���ı��Σ��ٸ����ı���OM'NH����������OP�ij����ٸ��ݵ�M������õ�PM'�ij���Rt��OPM'�У����ù��ɶ����ɵ�OM'��ֵ��������OM'��d=![]() �����ɵõ�d��ֵ��
�����ɵõ�d��ֵ��
�����������1����������![]() ��x�ύ��A����1��0����B��2��0�����㣬��
��x�ύ��A����1��0����B��2��0�����㣬��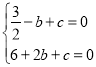 �������
������� �����������ߵĽ���ʽ
�����������ߵĽ���ʽ![]() ��
��
��2������ͼ������E��EE'��x����E'����EE'��OC����![]() ����BE=4EC����BE'=4OE'�����E������Ϊ��x��y������OE'=x��BE'=4x����B��2��0������OB=2����x+4x=2����x=
����BE=4EC����BE'=4OE'�����E��������x��y������OE'=x��BE'=4x����B��2��0������OB=2����x+4x=2����x=![]() ����������
����������![]() ��y�ύ�ڵ�C����C��0����3������ֱ��BC�Ľ���ʽΪy=kx+b'����B��2��0����C��0����3������
��y�ύ�ڵ�C����C��0����3������ֱ��BC�Ľ���ʽΪy=kx+b'����B��2��0����C��0����3������![]() �������
�������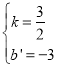 ����ֱ��BC�Ľ���ʽΪ
����ֱ��BC�Ľ���ʽΪ![]() ����x=
����x=![]() ʱ��y=��
ʱ��y=��![]() ����E��
����E��![]() ����
����![]() ������E���������ֱ��y=��x+n���ɵé�
������E���������ֱ��y=��x+n���ɵé�![]() +n=��
+n=��![]() �����n=��2��
�����n=��2��
�ڡ�AGF����CGDȫ�ȣ��������£�
��ֱ��EF�Ľ���ʽΪy=��x��2������y=0ʱ��x=��2����F����2��0����OF=2����A����1��0������OA=1����AF=2��1=1����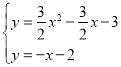 �������
�������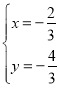 ��
��![]() ������D�ڵ������ޣ�����D������Ϊ��1����3��������C������Ϊ��0����3������CD��x�ᣬCD=1�����AFG=��CDG����FAG=��DCG�����AGF�ա�CGD��
������D�ڵ������ޣ�����D������Ϊ��1����3��������C������Ϊ��0����3������CD��x�ᣬCD=1�����AFG=��CDG����FAG=��DCG�����AGF�ա�CGD��
��3���������ߵĶԳ���Ϊx=![]() =
=![]() ��ֱ��y=m��m��0����������ߵĽ���ΪM��N������M��N����ֱ��x=
��ֱ��y=m��m��0����������ߵĽ���ΪM��N������M��N����ֱ��x=![]() �Գƣ���N��t��m������M��1��t��m�������� M����y��ĶԳƵ�Ϊ��M'����M'��t��1��m��������M'��ֱ��y=m�ϣ���M'N��x�ᣬ��M'N=t����t��1��=1����H��1��0������OH=1=M'N�����ı���OM'NH��ƽ���ı��Σ���ֱ��y=m��y�ύ�ڵ�P�����ı���OM'NH�����Ϊ
�Գƣ���N��t��m������M��1��t��m�������� M����y��ĶԳƵ�Ϊ��M'����M'��t��1��m��������M'��ֱ��y=m�ϣ���M'N��x�ᣬ��M'N=t����t��1��=1����H��1��0������OH=1=M'N�����ı���OM'NH��ƽ���ı��Σ���ֱ��y=m��y�ύ�ڵ�P�����ı���OM'NH�����Ϊ![]() ����OH��OP=1��m=
����OH��OP=1��m=![]() ����m=
����m=![]() ����OP=
����OP=![]() ����
����![]() =
=![]() ʱ�����x1=��
ʱ�����x1=��![]() ��x2=
��x2=![]() ������M����������
������M����������![]() ��
��![]() ������M'��
������M'��![]() ��
��![]() ������PM'=
������PM'=![]() ����Rt��OPM'��OM'=
����Rt��OPM'��OM'=![]() =
=![]() �����ı���OM'NH�����Ϊ
�����ı���OM'NH�����Ϊ![]() ����OM'��d=
����OM'��d=![]() ����d=
����d=![]() ��
��


 �ִʾ��ƪϵ�д�
�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ �� ������ABCD�У���ABC���BAD�Ķ�����Ϊ1��2���ܳ���32cm �� ��
��1�������Խ��ߵij��ȣ�
��2��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ת�������������û��̽�ԭ����������������������Ŵ����ʣ��������������Ƴ����Ӷ����Ʒ�ʸ��õ�����ҹ�����ת����������ֲ���ԼΪ4 200 000���꣬��4 200 000�ÿ�ѧ��������ʾΪ�� ��
A.4.2��106
B.4.2��105
C.42��105
D.0.42��107
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ��1�������dz����ġ���ͷͼ����������������Щ��ѧ֪ʶ�أ������������������⣺
��1���۲���ͼ��1������ͷͼ������̽����BDC���A����B����C֮���С�Ĺ�ϵ����˵�����ɣ�
��2������ֱ���������Ͻ��ۣ��ش������������⣺
����ͼ��2������һ�����ǰ�XYZ�����ڡ�ABC�ϣ�ʹ������ֱ�DZ�XY��XZǡ�þ�����B��C������A=50�㣬���ABX+��ACX
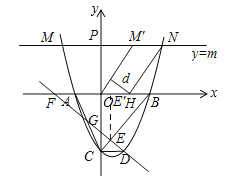
����ͼ��3������ABD����ACD����ȷ��߷ֱ��ཻ�ڵ�G1��G2��G3��G4 �� ����BDC=135�㣬��BG1C=67�㣬���A�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������֪�ġ�ABC�У������²�����ͼ��
�ٷֱ���B��CΪԲ�ģ��Դ���![]() BC�ij�Ϊ�뾶�����������ཻ������M��N��
BC�ij�Ϊ�뾶�����������ཻ������M��N��
����ֱ��MN��AB�ڵ�D������CD��
��CD=AC����A=50�㣬���ACB�Ķ���Ϊ��������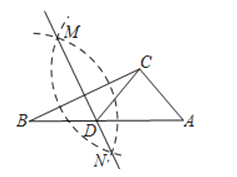
A.90��
B.95��
C.100��
D.105��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʹ����ֱ��������ȫ�ȵ������� ��
A. һ��ֱ�DZ���ԽǶ�Ӧ���
B. б�ߺ�һ��ֱ�DZ߶�Ӧ���
C. б�ߺ�һ��Ƕ�Ӧ���
D. ������Ƕ�Ӧ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Զ�����ȡ���дΪ�������������ô������������ʽ����дΪ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ï����������������������չ��ͷ���ã��ص���ĿͶ���ѳ���2000��Ԫ��2000��Ԫ�ÿ�ѧ��������ʾΪ��Ԫ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com