
����Ŀ����֪��������A��B�����㣮
��1����ͼ1����AB=a��M��AB���е㣬CΪ�߶�AB�ϵ�һ�㣬��![]() ����AC=�� ����CB=�� ����MC=�� �����ú�a�Ĵ���ʽ��ʾ����
����AC=�� ����CB=�� ����MC=�� �����ú�a�Ĵ���ʽ��ʾ����

��2����ͼ2����A��B��C�����Ӧ�����ֱ�Ϊ��40����10��20��
����A��C����ͬʱ�����˶���ͬʱB�������˶�����֪��A��B��C���ٶȷֱ�Ϊ8����λ����/�롢4����λ����/�롢2����λ����/�룬��MΪ�߶�AB���е㣬��NΪ�߶�BC���е㣬��B��C����ǰ�����˶�������ʱǡ�����㣺MB=3BN��
�����ж���P��Q����C���������P��ÿ��1����λ���ȵ��ٶ����յ�A�ƶ�������P�ƶ���B��ʱ����Q�Ŵ�C�����������ÿ��3����λ���ȵ��ٶ������ƶ����ҵ���P����A��ʱ����QҲֹͣ�ƶ��������P���˶�ʱ��Ϊt������PQ�����ľ���ǡΪ18����λʱ��������������ʱ��tֵ��
���𰸡���1��![]() a��
a��![]() a��
a��![]() a����2��2��ʱǡ������MB=3BN����3����tΪ18�롢36���54��ʱ��P��Q�������18����λ���ȣ�
a����2��2��ʱǡ������MB=3BN����3����tΪ18�롢36���54��ʱ��P��Q�������18����λ���ȣ�
��������
��1�����������еĵ�����ϵ��a��ʾ��AC,CB,MC���ɣ�
��2���ټ���x��C��B�ұ�ʱ��ǡ������MB=3BN���ݴ˵ó����̣����x��ֵ���ɣ�
�ڵ�P��ʾ����Ϊ20��t����Q��ʾ����Ϊ20��3��t��30�����ٷ�������ۢٵ���P�ƶ�18��ʱ���ڵ�Q�ڵ�P���Ҳ࣬�۵���Q�ڵ�P����࣬���ɵó�����.
�⣺��1����AB=a��CΪ�߶�AB�ϵ�һ�㣬��![]() =
=![]() ��
��
��AC=![]() AB=
AB=![]() a��CB=
a��CB=![]() AB=
AB=![]() a��
a��
��M��AB���е㣬
��MC=![]() AB��
AB��![]() AB=
AB=![]() a��
a��
�ʴ�Ϊ��![]() a��
a��![]() a��
a��![]() a��
a��
��2������A��B��C�����Ӧ�����ֱ�Ϊ��40����10��20��
��AB=BC=30��
��x��ʱ��C��B�ұ�ʱ��ǡ������MB=3BN��
��BM=![]() ��8x+4x+30����BN=
��8x+4x+30����BN=![]() ��30��4x��2x����
��30��4x��2x����
����MB=3BNʱ��![]() ��8x+4x+30��=3��
��8x+4x+30��=3��![]() ��30��4x��2x����
��30��4x��2x����
��ã�x=2��
��2��ʱǡ������MB=3BN��
��3����P��ʾ����Ϊ20��t����Q��ʾ����Ϊ20��3��t��30����
������P�ƶ�18��ʱ����Qû������ʱ��PQ�����ľ���ǡΪ18����λ��
����Q�ڵ�P���Ҳ࣬��20��3��t��30������20��t��=18��
���t=36��
������Q�ڵ�P����࣬��20��t��[20��3��t��30��]=18��
���t=54��
������������tΪ18�롢36���54��ʱ��P��Q�������18����λ���ȣ�


 ���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�п�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ��AB��CD�ཻ�ڵ�O����֪OEƽ����BOD������AOC����AOD=3��7��
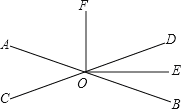
��1������DOE�Ķ�����
��2����OF��OE������COF�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2016.����ͼ��AD��BC�ཻ�ڵ�O��AD=BC����C=��D=90�㣮
��1������ABC=35�������CAO�Ķ�����
��2����֤��CO=DO
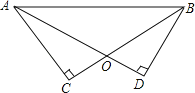
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c��x���һ��������A��1��0�����Գ���Ϊֱ��x=��1����һԪ���η���ax2+bx+c=0�Ľ��� �� 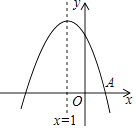
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ����������ֽ�еı���չ��ͼ�������������⣺
��1������ͼ�ϲ���һ��ͬ����С��������F��������Χ��һ�������壬������ ���ֲ�����
��2���뻭�����ֲ�ͬ�IJ�����
��3����A=a3+a2b+3��B=a2b��3��C=a3��1��D=6��a2b������2���е�չ��ͼΧ������������������Ĵ���ʽ֮�Ͷ���ȣ��ֱ���E��F�������Ĵ���ʽ��
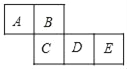
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ƽ���ڣ����κ���ͼ��Ķ���ΪA��1����4�����ҹ���B��3��0���� 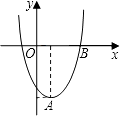
��1����ö��κ����Ľ���ʽ��
��2�����ö��κ���ͼ������ƽ�Ƽ�����λ����ʹƽ�ƺ�����ͼ������ԭ�㣿��ֱ��д��ƽ�ƺ�����ͼ����x�����һ����������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����CΪ�߶�AB��һ�㣬��ACM����CBN�ǵȱ������Σ�ֱ��AN��MC���ڵ�E��ֱ��BM��CN���ڵ�F�� 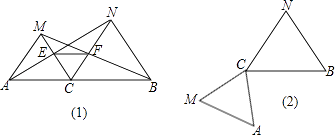
��1����֤��AN=MB��
��2����֤����CEFΪ�ȱ������Σ�
��3������ACM�Ƶ�C����ʱ�뷽����ת90�㣬�����������䣬�ڣ�2���л�������Ҫ���ͼ�Σ����жϣ�1����2�����е��������Ƿ���Ȼ��������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�����п�����A��B��C��D��E��λͬѧ����ѧ��Ӣ��ɼ����й���Ϣ���±���ʾ��
A | B | C | D | E | ƽ���� | ���� | |
��ѧ | 71 | 72 | 69 | 68 | 70 |
| |
Ӣ�� | 88 | 82 | 94 | 85 | 76 | 85 |
��1��������λͬѧ�ڱ��ο�������ѧ�ɼ���ƽ���ֺ�Ӣ��ɼ��ı��
��2��Ϊ�˱Ƚϲ�ͬѧ�ƿ��Գɼ��ĺ������ñ�����һ��������ѡ���ֵļ��㹫ʽ�DZ���=(���˳ɼ���ƽ���ɼ�)���ɼ���� �ӱ��ֿ������ִ�Ŀ��Գɼ����ã�����Aͬѧ�ڱ��ο����У���ѧ��Ӣ���ĸ�ѧ�ƿ��ø��ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�о���ʹ������ˮ�����±��շѣ�ˮ�Ѱ��½��ɣ���
������ˮ�� | ���� |
������12 m3�IJ��� | aԪ�Mm3 |
����12 m3��������20 m3�IJ��� | 1.5aԪ�Mm3 |
����20 m3�IJ��� | 2aԪ�Mm3 |
(1) ��a��2ʱ��ij�û�һ��������28 m3ˮ������û������Ӧ���ɵ�ˮ�ѣ�
(2) ��ij������ˮ��Ϊn �����ף���n��20ʱ������û�Ӧ���ɵ�ˮ��_____________Ԫ���ú�a��n����ʽ��ʾ����
(3) ��a��2ʱ���ס������û�һ���¹���ˮ40 m3����֪���û����ɵ�ˮ�ѳ�����24Ԫ������û��������ˮxm3��������ס������û�һ���¹����ɵ�ˮ�ѣ��ú�x����ʽ��ʾ����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com