
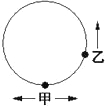
 速度是乙的
速度是乙的| 4 | 3 |
科目:初中数学 来源: 题型:
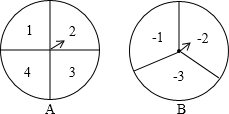
查看答案和解析>>
科目:初中数学 来源: 题型:
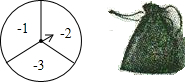 如图所示,甲、乙两人玩游戏,他们准备了1个可以自由转动的转盘和一个不透明的袋子.转盘被分成面积相等的三个扇形,并在每一个扇形内分别标上数字-1,-2,-3;袋子中装有除数字以外其它均相同的三个乒乓球,球上标有数字1,2,3.游戏规则:转动转盘,当转盘停止后,指针所指区域的数字与随机从袋中摸出乒乓球的数字之和为0时,甲获胜;其它情况乙获胜.(如果指针恰好指在分界线上,那么重转一次,直到指针指向某一区域为止)
如图所示,甲、乙两人玩游戏,他们准备了1个可以自由转动的转盘和一个不透明的袋子.转盘被分成面积相等的三个扇形,并在每一个扇形内分别标上数字-1,-2,-3;袋子中装有除数字以外其它均相同的三个乒乓球,球上标有数字1,2,3.游戏规则:转动转盘,当转盘停止后,指针所指区域的数字与随机从袋中摸出乒乓球的数字之和为0时,甲获胜;其它情况乙获胜.(如果指针恰好指在分界线上,那么重转一次,直到指针指向某一区域为止)查看答案和解析>>
科目:初中数学 来源: 题型:
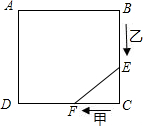 创新题:
创新题:| 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
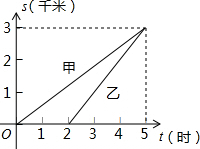 如图所示是甲、乙两人追赶过程中路程和时间之间的函数关系图象,由图象回答下列问题:
如图所示是甲、乙两人追赶过程中路程和时间之间的函数关系图象,由图象回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com