
分析 (1)先把分子和分母分解因式,再约分即可;
(2)先把分子和分母分解因式,再约分即可.
解答 解:(1)$\frac{{{a^2}-16}}{{{a^2}-8a+16}}$
=$\frac{(a+4)(a-4)}{(a-4)^{2}}$
=$\frac{a+4}{a-4}$,
故答案为:$\frac{a+4}{a-4}$;
(2)$\frac{{{x^2}-{{(y-z)}^2}}}{{{{(x+y)}^2}-{z^2}}}$
=$\frac{(x+y-z)(x-y+z)}{(x+y+z)(x+y-z)}$
=$\frac{x-y+z}{x+y+z}$,
故答案为:$\frac{x-y+z}{x+y+z}$.
点评 本题考查了最简分式,分式的基本性质的应用,能正确根据分式的基本性质进行约分是解此题的关键.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
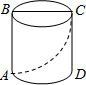 如图:一个圆柱的底面周长为16cm,高为6cm,BC是上底面的直径,一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,求蚂蚁爬行的最短路程(要求画出平面图形).
如图:一个圆柱的底面周长为16cm,高为6cm,BC是上底面的直径,一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,求蚂蚁爬行的最短路程(要求画出平面图形).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
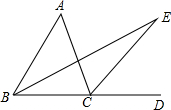 如图所示,∠ACD是△ABC的外角,∠A=40°,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E.
如图所示,∠ACD是△ABC的外角,∠A=40°,BE平分∠ABC,CE平分∠ACD,且BE、CE交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
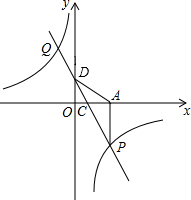 如图,一次函数y=kx+2的图象与反比例函数y=$\frac{m}{x}$的图象交于P、G两点,过点P作PA⊥x轴,一次函数图象分别交x轴、y轴于C、D两点,$\frac{CD}{CP}$=$\frac{1}{2}$,且S△ADP=6.
如图,一次函数y=kx+2的图象与反比例函数y=$\frac{m}{x}$的图象交于P、G两点,过点P作PA⊥x轴,一次函数图象分别交x轴、y轴于C、D两点,$\frac{CD}{CP}$=$\frac{1}{2}$,且S△ADP=6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com