
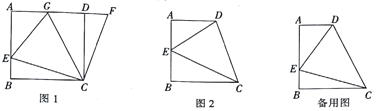
����Ŀ����ͼ1����������ABCD�У���E��AB��һ�㣬��F��AD�ӳ�����һ�㣬��DF=BE������CE��CF��
��1����֤��CE=CF��
��2����ͼ1�У�����G��AD�ϣ�����GCE=45�㣬��GE=BE+GD������Ϊʲô��
��3����������ѧ��֪ʶ�����ã�1������2������л��۵ľ��飬������и��⣬��ͼ2�����ı���ABCD�У�AD��BC��BC��AD������B=90�㣬AB=BC������DCE=45�㣮
����AE=6��DE=10����AB�ij���
����AB=BC=9��BE=3����DE�ij���
���𰸡���1��֤����������2��������3����12����7.5
��������
��1�����жϳ���B=��CDF�������жϳ���CBE�ա�CDE�����ɵó����ۣ�
��2�����жϳ���BCE=��DCF�������жϳ���ECF=��BCD=90�������ɵó���GCF=��GCE=45�����ó���ECG�ա�FCG���ɵó����ۣ�
��3�����жϳ�����ABCHΪ�����Σ������ó�AH=BC=AB��
�ٸ��ݹ��ɶ����ã�AD=8���ɣ�1����2��֪��ED=BE+DH����BE=x��������ʾ��DH=10-x����AH=AB�������̼��ɵó����ۣ�
���ɣ�1����2��֪��ED=BE+DH����DE=a��������ʾ��DH=a-3��AD=12-a��AE=6�����ݹ��ɶ�������������⼴�ɵó����ۣ�
��1����������ABCD��
��BC=CD����B=��ADC��
���B=��CDF��
��BE=DF��
���CBE�ա�CDF��
��CE=CF��
��2���������ɣ�1��֪����CBF�ա�CDE��
���BCE=��DCF��
���BCE+��ECD=��DCF+��ECD��
���ECF=��BCD=90�㣬
�ߡ�GCE=45�㣬
���GCF=��GCE=45�㣬
��CE=CF����GCE=��GCF��GC=GC��
���ECG�ա�FCG��
��GE=GF��
��GE=DF+GD=BE+GD��
��3����ͼ2������C��CH��AD��AD���ӳ�����H��
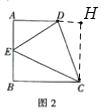
��AD��BC����B=90�㣬
���A=90�㣬
�ߡ�CHA=90�㣬
���ı���ABCHΪ���Σ�
��AB=BC��
�����ABCH������
��AH=BC=AB��
�١�AE=6��DE=10�����ݹ��ɶ����ã�AD=8��
�ߡ�DCE=45�㣬
�ɣ�1����2��֪��ED=BE+DH��
��BE=x��
��10+x=DH��
��DH=10-x��
��AH=AB��
��8+10-x=x+6��
��x=6��
��AB=12��
�ڡߡ�DCE=45�㣬
�ɣ�1����2��֪��ED=BE+DH��
��DE=a��
��a=3+DH��
��DH=a-3��
��AB=AH=9��
��AD=9-��a-3��=12-a��AE=AB-BE=6��
���ݹ��ɶ����ã�DE2=AD2+AE2��
������12-a��2+62=a2����a=7.5��
��DE=7.5��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��y=kx+b����A(0,2),B(4,0)����.
(1)��ֱ��AB��Ӧ�ĺ�������ʽ;
(2)����ֱ������ƽ��6����λ,��ƽ�ƺ��ֱ����x�ύ�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�κ���y=ax+c��a��0������κ���y=ax2+bx+c��a��0����ͬһƽ��ֱ������ϵ�е�ͼ������ǣ� ��
A.
B.
C.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˲μ�ѧУ���еĴ�ͳ�Ļ�֪ʶ������ij��������Ĵ�ģ��ѵ�������ɼ�����������������ʻ��Ƴ�����������������ͳ��ͼ��

![]()
��1���������� ��
��2�����ݼ��㣬���㲹ȫ����ͳ��ͼ��
��3���۲첹ȫ���ͳ��ͼ��д��һ���㷢�ֵĽ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1��2������4��+3
��2����32�£���2��3
��3����![]() ��
��![]() +
+![]() ����12
����12
��4����13+[����4��2����1��32����2]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���й�ʽ����·�������ѶԲ����й��˼��崳��������һ�ֵ�٩�������չ�һ���˾Ϳ������ˣ��ͺ��̵��ء������������ijý������ڶ��·�ڲɷô���Ƶ����ˣ��ó��γ�����������ĸ�����ԭ�ٺ��̵����ò���ѧ����ͨ�������ң��ڽ�����̬����ִ�����Ȳ������ܴ����������ü��߽���ε�����������������������в�������ͳ��ͼ������������Ϣ������������⣮ 
��1���ü��߱���һ�������������ˣ�
��2����ͼ1�Т��������ε�Բ�Ľǣ�����ȫͼ2��
��3���ڱ��ε����У���������ɷ����е�һ�����ˣ��������ڵڢ�������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ף����������2018�����ڣ�ijУ�������鷨���������������˲���ͬѧ�ijɼ���������������������������ͳ��ͼ��
������ | Ƶ�� | Ƶ�� |
60��x��70 | 30 | 0.15 |
70��x��80 | m | 0.45 |
80��x��90 | 60 | n |
90��x��100 | 20 | 0.1 |
���������ͼ���ṩ����Ϣ������������⣺
��1����ι��������� ����ѧ�������е���m=�� ����n=�� ����
��2���벹ȫƵ��ֱ��ͼ��
��3������������ͳ��ͼ���������60��x��70����Ӧ�����ε�Բ�ĽǵĶ������� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ������ϵ�У���֪��P����2����1������T��t��0����x���ϵ�һ�����㣮 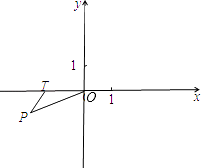
��1�����P����ԭ��ĶԳƵ�P������ꣻ
��2����tȡ��ֵʱ����P��TO�ǵ��������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y=��2m+1��x+m��3��
��1��������ͼ��ԭ�㣬��m��ֵ��
��2�������������һ�κ�������y����x���������С����m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com