Question

6．如图1，在平面直角坐标系中，O是坐标原点，?ABCD的顶点A的坐标为（-2，0），点D的坐标为（0，2$\sqrt{3}$），点B在x轴的正半轴上，点E为线段AD的中点，过点E的直线l与x轴交于点F，与射线DC交于点G．
（1）求∠DCB的度数；
（2）当点F的坐标为（-4，0）时，求点G的坐标；
（3）连接OE，以OE所在直线为对称轴，△OEF经轴对称变换后得到△OEF'，记直线EF'与射线DC的交点为H．
如图2，当点G在点H的左侧时，求证：△DEG∽△DHE．

Answer 1

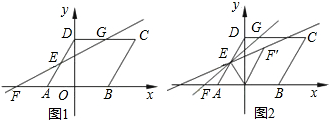
分析 （1）由于平行四边形的对角相等，只需求得∠DAO的度数即可，在Rt△OAD中，根据A、D的坐标，可得到OA、OD的长，那么∠DAO的度数就不难求了．
（2）根据点E、F的坐标求得直线EF的方程，然后将点G的纵坐标代入该直线方程即可求得点G的横坐标．
（3）根据A、D的坐标，易求得E点坐标，即可得到AE、OE的长，由此可判定△AOE是等边三角形，那么∠OEA=∠AOE=∠EOF′=60°，由此可推出OF′∥AE，即∠DEH=∠OF′E，根据轴对称的性质知∠OF′E=∠EFA，通过等量代换可得∠EFA=∠DGE=∠DEH，由此可证得所求的三角形相似．

解答 解：（1）在Rt△AOD中，
∵tan∠DAO=$\frac{DO}{AO}$=$\frac{2\sqrt{3}}{2}$=$\sqrt{3}$，
∴∠DAB=60°，
∵四边形ABCD是平行四边形，
∴∠DCB=∠DAB=60°．

（2）∵四边形ABCD是平行四边形，
∴CD∥AB，
∴∠DGE=∠AFE，
又∵∠DEG=∠AEF，DE=AE，
∴△DEG≌△AEF，
∴DG=AF
∵AF=OF-OA=4-2=2，
∴DG=2，
∴点G的坐标为（2，2$\sqrt{3}$），

（3）∵CD∥AB，
∴∠DGE=∠OFE，
∵△OEF经轴对称变换后得到△OEF′，
∴∠OFE=∠OF′E，
∴∠DGE=∠OF′E，
在Rt△AOD中，∵E是AD的中点，
∴OE=$\frac{1}{2}$AD=AE
又∵∠EAO=60°
∴∠EOA=60°，∠AEO=60°，
又∵∠EOF'=∠EOA=60°，
∴∠EOF′=∠OEA，
∴AD∥OF′，
∴∠OF′E=∠DEH，
∴∠DEH=∠DGE，
又∵∠HDE=∠EDG，
∴△DHE∽△DEG．

点评 本题考查平行四边形的性质、轴对称的性质、全等三角形以及相似三角形的判定和性质、锐角三角函数等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．