
【题目】如图,在△ABC中AB=AC,△AED中AE=AD,∠EAD=∠BAC,AC与BD交于点O.
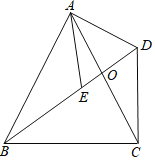
(1)试确定∠ADC与∠AEB间的数量关系,并说明理由;
(2)若∠ACB=65°,求∠BDC的度数.
【答案】(1)∠ADC=∠AEB,理由见解析;(2)50°
【解析】
(1)根据全等三角形的判定和性质证明即可;
(2)利用三角形的外角性质和三角形的内角和解答即可.
解:(1)∠ADC=∠AEB,理由如下:
∵∠BAC=∠EAD
∴∠BAC﹣∠EAC=∠EAD﹣∠EAC
即:∠BAE=∠CAD
在△ABE和△ACD中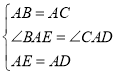
∴△ABE≌△ACD(SAS)
∴∠ADC=∠AEB
(2)∵∠BOC是△ABO和△DCO的外角
∴∠BOC=∠ABD+∠BAC,∠BOC=∠ACD+∠BDC
∴∠ABD+∠BAC=∠ACD+∠BDC
∵∠ABD=∠ACD
∴∠BAC=∠BDC
∵∠ACB=65°,AB=AC
∴∠ABC=∠ACB=65°
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣65°﹣65°=50°
∴∠BDC=∠BAC=50°


科目:初中数学 来源: 题型:
【题目】如图,![]() 点的坐标为
点的坐标为![]() ,
,![]() 点的坐标为
点的坐标为![]() ,
,![]() 点的坐标为
点的坐标为![]() ,
,![]() 点的坐标为
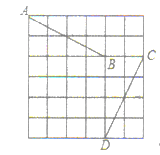
点的坐标为![]() ,小明发现:线段
,小明发现:线段![]() 与线段
与线段![]() 存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是_____________.
存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
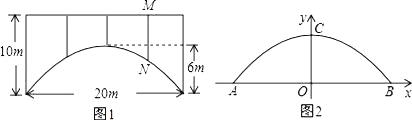
【题目】一座拱桥的轮廓是抛物线型(如图1所示),拱高6m,跨度20m,相邻两支柱间的距离均为5m.
(1)将抛物线放在所给的直角坐标系中(如图2所示),其表达式是y=ax2+c的形式.请根据所给的数据求出a,c的值.
(2)求支柱MN的长度.
(3)拱桥下地平面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道能否并排行驶宽2m、高3m的三辆汽车(汽车间的间隔忽略不计)?请说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示.下列结论:①方程=ax2+bx+c=0的两个根是x1=﹣1,x2=3:②a﹣b+c=0;③8a+c<0;④当y>0时,x的取值范围是﹣1<x<3;⑤当y随x的增大而增大时,一定有x<O.其中结论正确的个数是( )
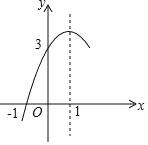
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
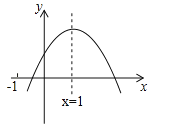
【题目】已知二次函数![]() 的图象如图所示,有以下结论:
的图象如图所示,有以下结论:
①abc>0,
②a﹣b+c<0,
③2a=b,
④4a+2b+c>0,
⑤若点(﹣2,![]() )和(
)和(![]() ,
,![]() )在该图象上,则
)在该图象上,则![]() .
.
其中正确的结论是 (填入正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
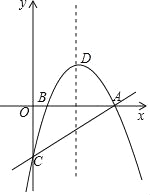
【题目】如图,抛物线y=ax2+bx+c与x轴交于A,B(1,0)两点,与y轴交于点C,直线y=![]() x﹣2经过A,C两点,抛物线的顶点为D.
x﹣2经过A,C两点,抛物线的顶点为D.
(1)求抛物线的解析式及顶点D的坐标;
(2)在直线AC上方的抛物线上存在一点P,使△PAC的面积最大,请直接写出P点坐标及△PAC面积的最大值;
(3)在y轴上是否存在一点G,使得GD+GB的值最小?若存在,求出点G的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
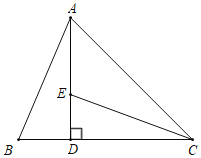
【题目】如图,在△ABC中,∠ACB=45°,过点A作AD⊥BC于点D,点E为AD上一点,且ED=BD.
(1)求证:△ABD≌△CED;
(2)若CE为∠ACD的角平分线,求∠BAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】制文中学2019年秋季在政大商场购进了![]() 、
、![]() 两种品牌的冰鞋,购买
两种品牌的冰鞋,购买![]() 品牌冰鞋花费了
品牌冰鞋花费了![]() 元,购买
元,购买![]() 品牌冰鞋花费了
品牌冰鞋花费了![]() 元,且购买
元,且购买![]() 品牌冰鞋的数量是购买
品牌冰鞋的数量是购买![]() 品牌冰鞋数量的
品牌冰鞋数量的![]() 倍,已知购买一双
倍,已知购买一双![]() 品牌冰鞋比购买一双
品牌冰鞋比购买一双![]() 品牌冰鞋多花
品牌冰鞋多花![]() 元.
元.
(1)求购买一双![]() 品牌,一双
品牌,一双![]() 品牌的冰鞋各需多少元?
品牌的冰鞋各需多少元?
(2)为开展好“冰雪进校园”活动,制文中学决定再次购买两种品牌冰鞋共![]() 双,如果这所中学这次购买
双,如果这所中学这次购买![]() 、
、![]() 两种品牌冰鞋的总费用不超过
两种品牌冰鞋的总费用不超过![]() 元,那么制文中学最多购买多少双
元,那么制文中学最多购买多少双![]() 品牌冰鞋?
品牌冰鞋?
查看答案和解析>>
科目:初中数学 来源: 题型:
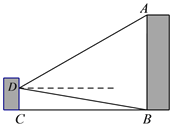
【题目】如图所示,某小组同学为了测量对面楼AB的高度,分工合作,有的组员测得两楼间距离为40米,有的组员在教室窗户处测得楼顶端A的仰角为30°,底端B的俯角为10°,请你根据以上数据,求出楼AB的高度.(精确到0.1米)
(参考数据:sin10°≈0.17, cos10°≈0.98, tan10°≈0.18, ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com