练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．（1）计算：（-4xy）•（xy+3x2y）
    （2）化简求值：（x-2y）（x+2y）-（x+1）2+3x．其中x=12，y=-2．

    分析 （1）根据单项式乘多项式的方法，计算（-4xy）•（xy+3x2y）即可．
    （2）首先化简（x-2y）（x+2y）-（x+1）2+3x，然后把x=12，y=-2代入化简后的算式，求出算式的值是多少即可．

    解答 解：（1）（-4xy）•（xy+3x2y）=-4x2y2-12x3y2．

    （2）（x-2y）（x+2y）-（x+1）2+3x
    =x2-4y2-x2-2x-1+3x
    =x-4y2-1
    当x=12，y=-2时，
    原式=12-4×（-2）2-1=12-16-1=-5

    点评 此题主要考查了整式的混合运算-化简求值，要熟练掌握，注意先按运算顺序把整式化简，再把对应字母的值代入求整式的值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

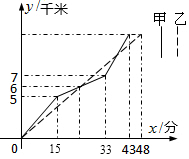    9．如图表示甲、乙两名同学在”五．一环遗爱湖自行车骑行”比赛中路程y（千米）随时间x（分）变化的图象（全程），根据图象回答下列问题．
    （1）当比赛开始多少分时，两人第一次相遇？
    （2）这次比赛全程是多少千米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．计算：
    （1）（$\sqrt{a}$+$\sqrt{b}$）（$\sqrt{a}$-$\sqrt{b}$）（a≥0，b≥0）
    （2）2$\sqrt{12}$+2$\sqrt{3}$-$\sqrt{48}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．如图，DA是∠BDF的平分线，∠3=∠4，若∠1=40°，∠2=140°，则∠CBD的度数为70°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．如图1，在正方形ABCD中，点P为AD延长线上一点，连接AC、CP，过点C作CF⊥CP于点C，交AB于点F，过点B作BM⊥CF于点N，交AC于点M．
    （1）若AP=$\frac{6}{5}$AC，BC=5，求S△ACP；
    （2）若CP-BM=2FN，求证：BC=MC；
    （3）如图2，在其他条件不变的情况下，将“正方形ABCD”改为“矩形ABCD”，且 AB≠BC，AC=AP，取CP中点E，连接EB，交AC于点O，猜想：∠AOB与∠ABM之间有何数量关系？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．一辆出租车从超市出发，向东走4千米到达小丽家，然后向西走2千米到达小华家，又向西走6千米达到小敏家，最后回到超市．

    （1）以超市为原点，规定向东为正方向，用1个单位长度表示1千米，你能在数轴上标出小丽家，小华家和小敏家的位置吗？
    （2）出租车一共行驶了多少千米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．计算：（-2）0+${（\frac{1}{2}）}^{-1}$=3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．（1）如图，在四边形ABCD中，∠A=104°-∠2，∠ABC=76°+∠2，BD⊥CD于D，EF⊥CD于F．
    求证：∠1=∠2．
    请你完成下面证明过程．
    证明：因为∠A=104°-∠2，∠ABC=76°+∠2，
    所以：∠A+∠ABC=104°-∠2+76°+∠2，即∠A+∠ABC=180°
    所以AD∥BC，（同旁内角互补，两直线平行）
    所以∠1=∠DBC，（两直线平行，内错角相等）
    因为BD⊥DC，EF⊥DC，
    所以∠BDC=90°，∠EFC=90°，（垂线的定义）
    所以∠BDC=∠EFC，
    所以BD∥EF，（同位角相等，两直线平行）
    所以∠2=∠DBC，（两直线平行，同位角相等）
    所以∠1=∠2（等量代换）．
    （2）如图，已知∠ABC=180°-∠A，BD⊥CD于D，EF⊥CD于F，①求证：AD∥BC．
    ②若∠1=36°，求∠2的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图，矩形OABC的顶点A、C分别在x、y轴的正半轴上，点B的坐标为（3，4），一次函数y=-$\frac{2}{3}$x+b的图象与边OC、AB分别交于点D、E，并且满足OD=BE，点M是线段DE上的一个动点．
    （1）求b的值；
    （2）连结OM，若△ODM的面积与四边形OAEM的面积之比为1：3，求点M的坐标；
    （3）设点N是x轴上方平面内的一点，当四边形OMDN为菱形时，求点N的坐标．

    查看答案和解析>>

    同步练习册答案