
����Ŀ������ΪD��������y����x2+bx+c��x����A��B(3��0)����y���ڵ�C��ֱ��y����![]() x+m������C����x����E(4��0)��
x+m������C����x����E(4��0)��
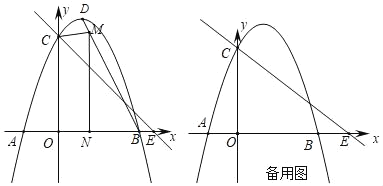
(1)��������ߵĽ���ʽ��
(2)��ͼ1����MΪ�߶�BD�ϲ���B��D�غϵ�һ�����㣬����M��x��Ĵ��ߣ�����ΪN�����M�ĺ�����Ϊx���ı���OCMN�����ΪS����S��x֮��ĺ�����ϵʽ������S�����ֵ��
(3)��PΪx�����������һ�����㣬��P��x��Ĵ��ߣ���ֱ��y����![]() x+m��G������������H������CH������CGH��CH���ۣ�����G�Ķ�Ӧ��Fǡ������y����ʱ����ֱ��д����P�����꣮
x+m��G������������H������CH������CGH��CH���ۣ�����G�Ķ�Ӧ��Fǡ������y����ʱ����ֱ��д����P�����꣮
���𰸡�(1)y����x2+2x+3��(2)S����(x��![]() )2+
)2+![]() ����x��
����x��![]() ʱ��S�����ֵ�����ֵΪ
ʱ��S�����ֵ�����ֵΪ![]() ��(3)���ڣ���P������Ϊ(4��0)��(
��(3)���ڣ���P������Ϊ(4��0)��(![]() ��0).
��0).
��������
��1������E����ֱ�߽���ʽ�У��������C�����꣬����C��B���������߽���ʽ�У�����������߽���ʽ��
��2���������߽���ʽ��ɶ���ʽ���������D�����꣬��ֱ��BD�Ľ���ʽ�������B��D�������ֱ��BD�Ľ���ʽ����MN�ɱ�ʾ����S�ɱ�ʾ��
��3�����P�����꣬���G������ɱ�ʾ����H������ɱ�ʾ��HG���ȿɱ�ʾ�����÷����Ƴ�CG��HG���е�ʽ��⼴�ɣ�
��1������E����ֱ�߽���ʽ�У�
0����![]() ��4+m��
��4+m��
���m��3��
�����ʽΪy����![]() x+3��
x+3��
��C(0��3)��
��B(3��0)��
����![]() ��
��
���![]() ��
��
�������ߵĽ���ʽΪ��y����x2+2x+3��
��2����y����x2+2x+3����(x��1)2+4��
��D(1��4)��
��ֱ��BD�Ľ���ʽΪy��kx+b�������B��D��
![]() ��
��
���![]() ��
��
��ֱ��BD�Ľ���ʽΪy����2x+6��
���M������Ϊ(x����2x+6)��
��S��(3+6��2x)x![]() ����(x��
����(x��![]() )2+
)2+![]() ��
��
�൱x��![]() ʱ��S�����ֵ�����ֵΪ
ʱ��S�����ֵ�����ֵΪ![]() ��
��
(3)���ڣ�
��ͼ��ʾ��
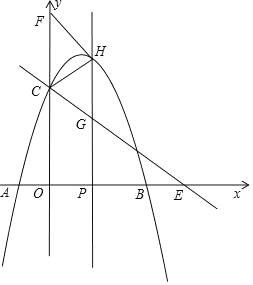
���P������Ϊ(t��0)��
���G(t����![]() t+3)��H(t����t2+2t+3)��
t+3)��H(t����t2+2t+3)��
��HG��|��t2+2t+3��(��![]() t+3)|��|t2��
t+3)|��|t2��![]() t|
t|
CG��![]() ��
��![]() t��
t��
�ߡ�CGH��GH���ۣ�G�Ķ�Ӧ��Ϊ��F��F����y���ϣ�
��HG��y�ᣬ
��HG��CF��HG��HF��CG��CF��
��GHC����CHF��
���FCH����CHG��
���FCH����FHC��
���GCH����GHC��
��CG��HG��
��|t2��![]() t|��
t|��![]() t��
t��
��t2��![]() t��
t��![]() tʱ��
tʱ��
���t1��0(��)��t2��4��
��ʱ��P(4��0)��
��t2��![]() t����
t����![]() tʱ��
tʱ��
���t1��0(��)��t2��![]() ��
��
��ʱ��P(![]() ��0)��
��0)��
���ϣ���P������Ϊ(4��0)��(![]() ��0)��
��0)��


 ����С��ʿ���������ϵ�д�
����С��ʿ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У����κ���![]() ��ͼ����ͼ���ָ������н��ۣ���
��ͼ����ͼ���ָ������н��ۣ���![]() ����
����![]() ����
����![]() ����
����![]() ����
����![]() ��������Ϊ
��������Ϊ![]() ��
��![]() ��������ȷ�Ľ����У� ��
��������ȷ�Ľ����У� ��
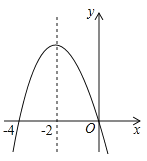
A.�٢ۢ�B.�ڢܢ�C.�٢ڢ�D.�ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���![]() �У���
�У���![]() ΪԲ�ģ�
ΪԲ�ģ�![]() ��Ϊ�뾶������
��Ϊ�뾶������![]() �ڵ�
�ڵ�![]() ���ֱ��Ե�
���ֱ��Ե�![]() ��
��![]() ΪԲ�ģ�����
ΪԲ�ģ�����![]() �ij�Ϊ�뾶�������������ڵ�
�ij�Ϊ�뾶�������������ڵ�![]() ������AG���ӳ���
������AG���ӳ���![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() .��
.��![]() ��
��![]() �������н��ۣ����ı���
�������н��ۣ����ı���![]() �����Σ���
��������![]() ����
����![]() ����
����![]() ����
����![]() .��ȷ���У����� ��
.��ȷ���У����� ��

A.�٢ۢ�B.�٢ۢ�C.�ڢۢܢ�D.�٢ڢۢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
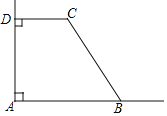
����Ŀ����ͼ��ʾ��AB��AD�ڵ�A��CD��AD�ڵ�D����C��120�������߶�BC��CD�ĺ�Ϊ12�����ı���ABCD����������ǣ�������
A.24![]() B.30
B.30![]() C.45D.
C.45D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
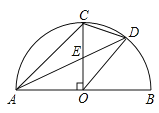
����Ŀ����ͼ��AB�ǰ�ԲO��ֱ�����뾶OC��AB�ڵ�O����D��![]() ���е㣬����CD��OD�������ĸ����ۣ���AC
���е㣬����CD��OD�������ĸ����ۣ���AC![]() OD����CE=OE������ODE����ADO���ܡ�ADC=��BOD��������ȷ���۵�����ǣ� ��
OD����CE=OE������ODE����ADO���ܡ�ADC=��BOD��������ȷ���۵�����ǣ� ��
A.�٢�B.�٢ڢ�C.�ڢ�D.�٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����ⷢ��
��ͼ�٣���ABC�͡�AED���ǵ���ֱ�������Σ���BAC=��EAD=90������B���߶�AE�ϣ���C���߶�AD�ϣ���ֱ��д���߶�BE���߶�CD��������ϵ�� ��
��2������̽��
��ͼ�ڣ���ͼ���еġ�ABC�Ƶ�A˳ʱ����ת����ת��Ϊ����0��![]() ��
��![]() 360���������жϲ�֤���߶�BE���߶�CD��������ϵ��
360���������жϲ�֤���߶�BE���߶�CD��������ϵ��
��3���������
��ͼ���еġ�ABC�Ƶ�A˳ʱ����ת����ת��Ϊ����0��![]() ��
��![]() 360��������DE=2AC������ת�Ĺ����У�����A��B��C��D�ĵ�Ϊ������ı�����ƽ���ı���ʱ����ֱ��д����ת�����Ķ��� ��
360��������DE=2AC������ת�Ĺ����У�����A��B��C��D�ĵ�Ϊ������ı�����ƽ���ı���ʱ����ֱ��д����ת�����Ķ��� ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������C��1��2���ֱ���x�ᡢy���ƽ���ߣ���ֱ��y����x+8��A��B���㣬������������y��![]() ��x��0����ͼ�����ABC�й����㣬��k��ȡֵ��Χ��_____��
��x��0����ͼ�����ABC�й����㣬��k��ȡֵ��Χ��_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BD��������ABCD�ĶԽ��ߣ�BC=4����BC�������ڵ�ֱ����ƽ�ƣ�ƽ�ƺ�õ����߶μ�ΪPQ������PA��QD��������Q��QO��BD������ΪO������OA��OP��
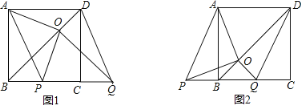
��1����ֱ��д���߶�BC��ƽ�ƹ����У��ı���APQD��ʲô�ı��Σ�
��2�����ж�OA��OP֮���������ϵ��λ�ù�ϵ��������ͼ1����֤����
��3����ƽ�Ʊ任�����У���y=S��OPB��BP=x(0��x��4)����y��x֮��ĺ�����ϵʽ�������y�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�ǡ�ABC��AB����һ�㣬�Ե�OΪԲ�ģ�OA�ij�Ϊ�뾶����O����Oǡ�þ�����C�������BC��AB�ֱ���E��F���㣮����AE������E����O�����ߣ����߶�BF�ڵ�M����AC���ӳ����ڵ�N����EM=BM��EB=AO��
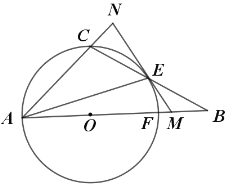
��1����![]() �Ķ�����
�Ķ�����
��2����֤��![]() ��
��
��3����![]() ����
����![]() �������
�������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com