
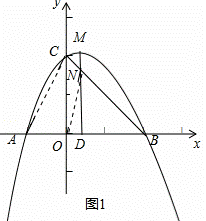
已知抛物线y=ax2+x+c(a≠0)经过A(﹣1,0),B(2,0)两点,与y轴相交于点C,该抛物线的顶点为点M,对称轴与BC相交于点N,与x轴交于点D.
(1)求该抛物线的解析式及点M的坐标;
(2)连接ON,AC,证明:∠NOB=∠ACB;
(3)点E是该抛物线上一动点,且位于第一象限,当点E到直线BC的距离为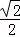 时,求点E的坐标;
时,求点E的坐标;
(4)在满足(3)的条件下,连接EN,并延长EN交y轴于点F,E、F两点关于直线BC对称吗?请说明理由.

解:(1)∵抛物线y=ax2+x+c(a≠0)经过A(﹣1,0),B(2,0)两点,
∴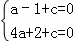 ,
,
解得 .
.
∴抛物线为y=﹣x2+x+2;
∴抛物线为y=﹣x2+x+2=﹣(x﹣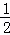 )2+
)2+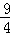 ,
,
∴顶点M(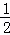 ,
,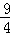 ).
).
(2)如图1,∵A(﹣1,0),B(2,0),C(0,2),
∴直线BC为:y=﹣x+2,
当x=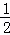 时,y=
时,y=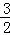 ,
,
∴N(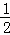 ,
,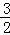 ),
),
∴AB=3,BC=2 ,OB=2,BN=
,OB=2,BN=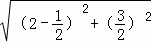 =
=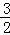
 ,
,
∴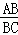 =
=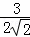 =
=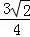 ,
,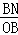 =
= =
=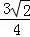 ,
,
∵∠ABC=∠NBO,
∴△ABC∽△NBO,
∴∠NOB=∠ACB;
(3)如图2,作EF⊥BC于F,
∵直线BC为y=﹣x+2,
∴设E(m,﹣m2+m+2),直线EF的解析式为y=x+b,
则直线EF为y=x+(﹣m2+2),
解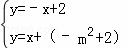 得
得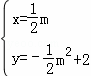 ,
,
∴F(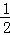 m2,﹣
m2,﹣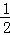 m2+2),
m2+2),
∵EF=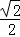 ,
,
∴(m﹣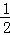 m2)2+(﹣
m2)2+(﹣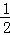 m2+2+m2﹣m﹣2)2=(
m2+2+m2﹣m﹣2)2=( )2,
)2,
解得m=1,
∴﹣m2+m+2=2,
∴E(1,2),
(4)如图2,延长EF交y轴于Q,
∵m=1,
∴直线EF为y=x+1,
∴Q(0,1),
∵F( ,
,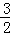 ),
),
∴FQ=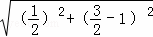 =
= ,
,
∵EF= ,EF⊥BC,
,EF⊥BC,
∴E、F两点关于直线BC对称.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
小军家距学校5千米,原来他骑自行车上学,学校为保障学生安全,新购进校车接送学生,若校车速度是他骑自行车速度的2倍,现在小军乘班车上学可以从家晚出发,结果与原来到校的时间相同.设小军骑车的速度为x千米/时,则所列方程正确的为
(A)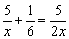 . (B)
. (B) .
.
(C) . (D)
. (D) .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,甲建筑物的高AB为40m,AB⊥BC,DC⊥BC,某数学学习小组开展测量乙建筑物高度的实践活动,从B点测得D点的仰角为60°,从A点测得D点的仰角为45°.求乙建筑物的高DC.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
有四张正面分别标有数字2,1,﹣3,﹣4的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上,洗匀后从四张卡片中随机地摸取一张不放回,将该卡片上的数字记为m,再随机地摸取一张,将卡片上的数字记为n.
(1)请画出树状图并写出(m,n)所有可能的结果;
(2)求所选出的m,n能使一次函数y=mx+n的图象经过第二、三、四象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
某校有25名同学们参加某比赛,预赛成绩各不同,要取前13名参加决赛,小明已经知道了自己的成绩,他想知道自己能否进入决赛,只需要再知道这25名同学成绩的( )
A. 最高分 B. 中位效 C. 极差 D. 平均数
查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系中横、纵坐标均是整数的点称为整点,例如点(-1,4)是一个整点.直线y=-x+4与两坐标轴围成△AOB,点P是△AOB的边及其内部的整点,则点P落在以O为圆心,3为半径的圆内的概率为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com