
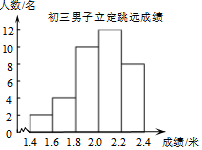
 ��ͼ��ΪijУ��������������Զ�ɼ���ͳ��ͼ�������Ҹ������ε�����֮��Ϊ1��2��5��6��4���������Ƶ����12���������������˵��
��ͼ��ΪijУ��������������Զ�ɼ���ͳ��ͼ�������Ҹ������ε�����֮��Ϊ1��2��5��6��4���������Ƶ����12���������������˵��| A�� | �٢� | B�� | �٢� | C�� | �ڢ� | D�� | �ڢ� |
���� ���õ���С���Ƶ����������ռ�İٷֱȼ�����ò��Ե�������
�ڸ���������ȷ����λ����λ�ü��ɣ�
�ۼ���ƽ������ȷ������
�ܸ�������ȷ�����ϸ���������ɣ�
��� �⣺�١ߴ����Ҹ������ε�����֮��Ϊ1��2��5��6��4���������Ƶ����12��
����Ե�������Ϊ12��$\frac{6}{1+2+5+6+4}$=36����ȷ��
�ڹ�36�ˣ���λ��Ӧ�ǵ�18�͵�19�˵�ƽ������
����λ������2.0-2.2С�飬�ʴ���
��������Զ�ɼ���ƽ����Ϊ$\frac{2��1.5+4��1.7+10��1.9+12��2.1+8��2.3}{36}$��2.01������ȷ��
�ܵ���1.8����6�ˣ�����1.85�IJ�ȷ�����ʴ���
��ѡA��
���� ���⿼����Ƶ�����ʣ��ֲ�ֱ��ͼ���Լ��������������壬Ū�������ǽⱾ��Ĺؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x+1��y+1 | B�� | x2��y2 | C�� | $\frac{x}{2}��\frac{y}{2}$ | D�� | 2x��2y |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{3}$ | B�� | $\frac{2}{9}$ | C�� | $\frac{4}{9}$ | D�� | $\frac{3}{10}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
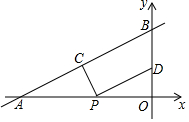 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=$\frac{2}{3}$x+4��x�ᡢy��ֱ��ڵ�A�͵�B����C��D�ֱ�Ϊ�߶�AB��OB���е㣬����PΪOA��һ���㣬��PC+PDֵ��СʱOP�ij�Ϊ��������
��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=$\frac{2}{3}$x+4��x�ᡢy��ֱ��ڵ�A�͵�B����C��D�ֱ�Ϊ�߶�AB��OB���е㣬����PΪOA��һ���㣬��PC+PDֵ��СʱOP�ij�Ϊ��������| A�� | 3 | B�� | 6 | C�� | $\frac{2}{3}$ | D�� | $\frac{3}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3.14 | B�� | $\frac{1}{3}$ | C�� | $\sqrt{9}$ | D�� | $\sqrt{6}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com