
����Ŀ����ͼ�٣���һ��ֱ�����ǰ����ͬһ��ֱ��AB�ϣ����С�ONM=30�㣬��OCD=45�㣮
��1����ͼ���е����ǰ�OMN��BA�ķ���ƽ����ͼ�ڵ�λ�ã�MN��CD�ཻ�ڵ�E�����CEN�Ķ�����
��2����ͼ���е����ǰ�OMN�Ƶ�O����ʱ�뷽����ת����ͼ�ۣ�����CON=5��DOMʱ��MN��CD�ཻ�ڵ�E�������ж�MN��BC��λ�ù�ϵ�������CEN�Ķ���
��3����ͼ���е����ǰ�OMN�Ƶ�O��ÿ��5����ٶȰ���ʱ�뷽����תһ�ܣ�����ת�Ĺ����У����ǰ�MON�˶������ֱ��MNǡ����ֱ��CDƽ�У�
��4������ͼ��λ�õ��������ǰ�ͬʱ�Ƶ�O��ʱ����ת���ٶȷֱ�ÿ��20���ÿ��10�㣬������һ�����ǰ�ص���ʼλ��ʱ���������ǰ�ͬʱֹͣת����������������OC���ON���ഹֱ����ֱ��д���𰸣�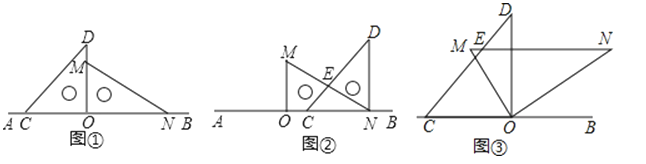
���𰸡��⣺��1���ڡ�CEN�У���CEN=180�㩁30�㩁45��=105�㣻
��2����ͼ�ڣ��ߡ�CON=5��DOM
��180�㩁��DOM=5��DOM��
���DOM=30��
�ߡ�OMN=60�㣬
��MN��OD��
��MN��BC��
���CEN=180�㩁��DCO=180�㩁45��=135�㣻
��3����ͼ�ۣ�MN��CDʱ����ת��Ϊ90�㩁��60�㩁45�㣩=75�㣬
��270�㩁��60�㩁45�㣩=255�㣬
���ԣ�t=75���5��=15�룬
��t=255���5��=51�룻
���ԣ�����ת�Ĺ����У����ǰ�MON�˶�15���51���ֱ��MNǡ����ֱ��CDƽ�У�
��4��MN��CDʱ����ת�ǵĽǶȲ���90�㣬
����90��£�20�㩁10�㣩=9�룬
�ʴ�Ϊ��9��
����������1�����������ε��ڽǺͶ�����ʽ���㼴�ɵý⣻
��2�����MN��OD��Ȼ�����ͬλ����ȣ���ֱ��ƽ���жϳ�MN��BC���ٸ�����ֱ��ƽ�У�ͬ���ڽǻ������
��3����������������ת�ǣ��ٸ���ʱ��=��ת�ǡ��ٶȼ��㼴�ɵý⣮
��4�������ת�ĽǶȲ�ٸ���ʱ��=��ת�Dz���ٶȲ���㼴�ɵý⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ƥ���������������ڽ�������һ�ڡ�����һԲ����Ͷ��35��Ԫ������35��Ԫ�ÿ�ѧ��������ʾΪ�� ��
A.0.35��1010Ԫ
B.3.5��108Ԫ
C.3.5��109Ԫ
D.35��108Ԫ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʵ��̽����
��1�����ֲ�����
����ͼ1����һ��ֱ�����ǰ�DEF������ֱ�����ǰ�ABC�ϣ�ʹ���ǰ�DEF������ֱ�DZ�DE��DF�ֱ���B��C����BC��EF����֪��A=30�㣬���ABD+��ACD=
����ͼ2����ֱ�����ǰ�ABC�������ı����ֱ�����ǰ�DEF��λ�ã�ʹ���ǰ�DEF������ֱ�DZ�DE��DF��Ȼ�ֱ���B��C����ô��ABD+��ACD= 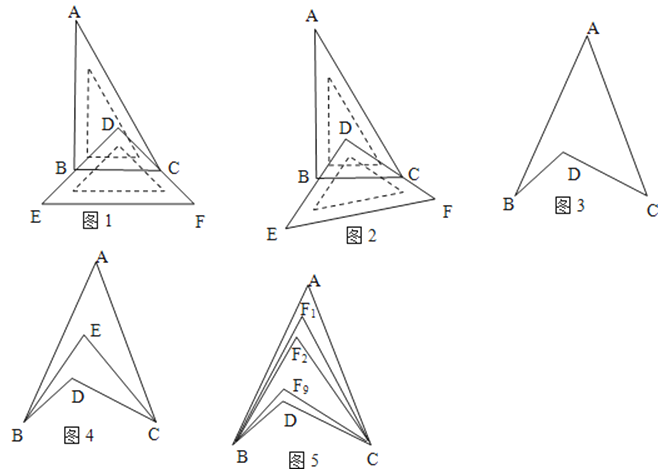
��2������֤����
��ͼ3����BDC���A����B����C֮������� ��ϵ
��3�����Ӧ�ã�
����ֱ���������Ͻ��ۣ�������������⣺
����ͼ4��BEƽ�֡�ABD��CEƽ�֡�ACB������BAC=40�㣬��BDC=120�㣬��BEC
����ͼ5����ABD����ACD��10�ȷ����ཻ�ڵ�F1��F2������F9 ��
����BDC=120�㣬��BF3C=64�㣬���A�Ķ���Ϊ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�� һ�κ�����ͼ����x����y��ֱ��ཻ�ڵ�A��B������AOB��ֱ��AB����������ACB.����C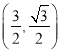 �����һ�κ����ı���ʽ��
�����һ�κ����ı���ʽ��
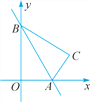
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����a=����2013��0 �� b=����0.5����1 �� c=����![]() ����2 �� ��a��b��c�Ĵ�СΪ��������
����2 �� ��a��b��c�Ĵ�СΪ��������
A.a��c��b
B.c��b��a
C.c��a��b
D.a��b��c
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ������ʵ���У��ס�����������ȼ��ʱʣ�ಿ�ֵĸ߶�![]() ��cm����ȼ��ʱ��
��cm����ȼ��ʱ��![]() ��h���Ĺ�ϵ��ͼ��ʾ. �����ͼ�����ṩ����Ϣ������и����⣺
��h���Ĺ�ϵ��ͼ��ʾ. �����ͼ�����ṩ����Ϣ������и����⣺

��1��������������ȼ��ǰ�ĸ߶ȷֱ��� ���ӵ�ȼ��ȼ�����õ�ʱ��ֱ��� ��
��2���ֱ�����ס�����������ȼ��ʱ![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��3����![]() Ϊ��ֵʱ���ס�������������ȼ�յĹ����еĸ߶���ȣ�
Ϊ��ֵʱ���ס�������������ȼ�յĹ����еĸ߶���ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���A�������ǣ�4����3��������A����x��ĶԳƵ㣬�õ���A����������A������y��ĶԳƵ㣬�õ���A�������A����������_____��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com