
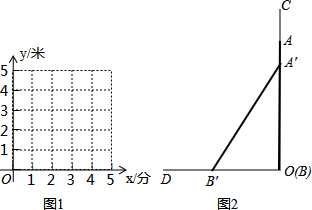
分析 (1)在Rt△A′OB′中,根据勾股定理求出OB′即可.
(2)在Rt△A′OB′中,根据勾股定理即可解决问题,再根据题意写出自变量的取值范围.
(3)①先列表,再画出图象即可.②利用两点间距离公式即可解决问题.
(4)如图2中,在半径OQ上取AB=BC,过A、B、C作x轴的垂线交圆弧于D、E、F,作DM⊥BE,EN⊥CF,延长DE交CF于G,只要证明EM>FN即可解决问题.
解答 解:(1)x=1时,A′B=5-1=4,A′B′=5,
∵∠O=90°,
∴y=OB′=$\sqrt{A′B{′}^{2}-A′{O}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3.
故答案为3.
(2)y=$\sqrt{{5}^{2}-(5-x)^{2}}$=$\sqrt{10x-{x}^{2}}$,(0≤x≤5).
(3)①填表: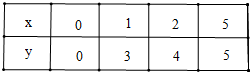
②图象如图所示: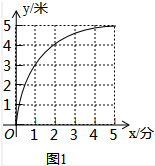
∵y=$\sqrt{{5}^{2}-(5-x)^{2}}$,
∴y2+(5-x)2=52,
即PQ2=PR2+RQ2=25,
∴PQ=5,
∴P到点Q(5,0)的距离是定值
(4)与(3)可知,函数图象是以Q为圆心的圆弧,
如图2中,在半径OQ上取AB=BC,过A、B、C作x轴的垂线交圆弧于D、E、F,作DM⊥BE,EN⊥CF,延长DE交CF于G.那么GN=EM,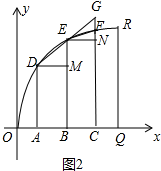
∵GN>FN,
∴EM>FN,
即点A移动的距离大于点B移动的距离,
∴是减速,
故选C.
点评 本题考查圆的综合题、勾股定理,列表法画函数图象等知识,解题的关键是学会构建函数解决问题,学会画好图象,利用图象思考问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,E(8,0),F(0,6).
如图,在平面直角坐标系xOy中,E(8,0),F(0,6).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知抛物线y=x2-(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴分别交于D、E两点
如图,已知抛物线y=x2-(m+3)x+9的顶点C在x轴正半轴上,一次函数y=x+3与抛物线交于A、B两点,与x、y轴分别交于D、E两点查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 去年“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,在个人反思、同伴互助总结后,向乌龟挑战再赛一场.这一次担任裁判的马大哥根据“他们两个”在奔跑能力方面的差异,制订了特殊的比赛规则(兔子必须让乌龟先跑一段时间).图中的函数图象刻画了“龟兔再次赛跑”的情景.
去年“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,在个人反思、同伴互助总结后,向乌龟挑战再赛一场.这一次担任裁判的马大哥根据“他们两个”在奔跑能力方面的差异,制订了特殊的比赛规则(兔子必须让乌龟先跑一段时间).图中的函数图象刻画了“龟兔再次赛跑”的情景.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com