
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 于
于![]() ,
,![]() 在
在![]() 上,连接
上,连接![]() ,
,![]() ,延长
,延长![]() 与
与![]() 的延长线交于
的延长线交于![]() ,
,![]() 在
在![]() 上,且
上,且![]() .
.
![]() 求证:
求证:![]() 是
是![]() 的切线;
的切线;
![]() 若
若![]() ,
,![]() ,求
,求![]() 的长.
的长.
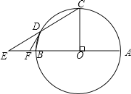
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)连结OD,由CO⊥AB得∠E+∠C=90°,根据等腰三角形的性质由FE=FD,OD=OC得到∠E=∠FDE,∠C=∠ODC,于是有∠FDE+∠ODC=90°,则可根据切线的判定定理得到FD是⊙O的切线;
(2)连结AD,如图,利用圆周角定理,由AB为⊙O的直径得到∠ADB=90°,则∠A+∠ABD=90°,加上∠OBD=∠ODB,∠BDF+∠ODB=90°,则∠A=∠BDF,易得△FBD∽△FDA,根据相似的性质得![]() ,再在Rt△ABD中,根据正切的定义得到tan∠A=tan∠BDF=
,再在Rt△ABD中,根据正切的定义得到tan∠A=tan∠BDF=![]() =
=![]() ,于是可计算出DF=2,从而得到EF=2.
,于是可计算出DF=2,从而得到EF=2.
![]() 连结
连结![]() ,如图,
,如图,
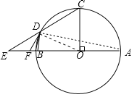
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是
是![]() 的切线;
的切线;
![]() 连结
连结![]() ,如图,
,如图,
∵![]() 为
为![]() 的直径,
的直径,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
而![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】如图在Rt△ABC中,∠C=90°,点D是AC的中点,且∠A+∠CDB=90°,过点A、D作⊙O,使圆心O在AB上,⊙O与AB交于点E.

(1)求证:直线BD与⊙O相切;
(2)若AD:AE=4:5,BC=6,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在△ABC中,AB=BC=4,∠ABC=90°,M是AC的中点,点N在AB上(不同于A、B),将△ANM绕点M逆时针旋转90°得△A1PM.
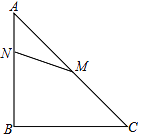
(1)画出△A1PM
(2)设AN=x,四边形NMCP的面积为y,直接写出y关于x的函数关系式,并求y的最大或最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线BC与半径为6的⊙O相切于点B,点M是圆上的动点,过点M作MC⊥BC,垂足为C,MC与⊙O交于点D,AB为⊙O的直径,连接MA、MB,设MC的长为x,(6<x<12).
(1)当x=9时,求BM的长和△ABM的面积;
(2)是否存在点M,使MDDC=20?若存在,请求出x的值;若不存在,请说明理由.
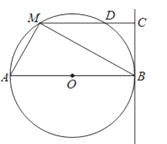
查看答案和解析>>
科目:初中数学 来源: 题型:
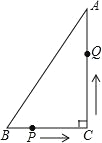
【题目】如图,在Rt△ABC中,AC=8cm,BC=6cm,P点在BC上,从B点到C点运动(不包括 C点),点 P运动的速度为1cm/s;Q点在AC上从C点运动到A点(不包括A点),速度为2cm/s,若点 P、Q 分别从B、C 同时运动,且运动时间记为t秒,请解答下面的问题,并写出探索的主要过程.
(1)当 t 为何值时,P、Q 两点的距离为 4![]() cm?
cm?
(2)请用配方法说明,点P运动多少时间时,四边形BPQA的面积最小?最小面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.
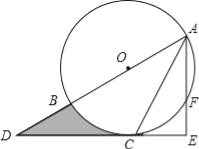
(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B,C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB∶S四边形CBFG=1∶2;③∠ABC=∠ABF;④AD2=FQ·AC,其中正确结论的个数是( )
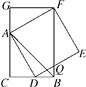
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
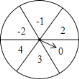
【题目】如图是一个被平均分成![]() 等份的转盘,每一个扇形中都标有相应的数字,甲乙两人分别转动转盘,设甲转动转盘后指针所指区域内的数字为
等份的转盘,每一个扇形中都标有相应的数字,甲乙两人分别转动转盘,设甲转动转盘后指针所指区域内的数字为![]() ,乙转动转盘后指针所指区域内的数字为
,乙转动转盘后指针所指区域内的数字为![]() (当指针在边界上时,重转一次,直到指向一个区域为止).
(当指针在边界上时,重转一次,直到指向一个区域为止).
![]() 直接写出甲转动转盘后所指区域内的数字为负数的概率;
直接写出甲转动转盘后所指区域内的数字为负数的概率;
![]() 用树状图或列表法,求出点
用树状图或列表法,求出点![]() 落在第二象限内的概率.
落在第二象限内的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一张透明的平行四边形胶片沿对角线剪开,得到图①中的两张三角形胶片![]() 和
和![]() .将这两张三角形胶片的顶点B与顶点E重合,把
.将这两张三角形胶片的顶点B与顶点E重合,把![]() 绕点B顺时针方向旋转,这时AC与DF相交于点O.
绕点B顺时针方向旋转,这时AC与DF相交于点O.
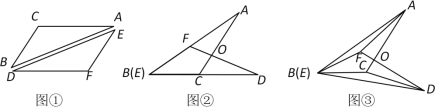
(1)当![]() 旋转至如图②位置,点B(E),C,D在同一直线上时,∠AFD与∠DCA的数量关系是 .
旋转至如图②位置,点B(E),C,D在同一直线上时,∠AFD与∠DCA的数量关系是 .
(2)当![]() 继续旋转至如图③位置时,(1)中的结论还成立吗?请说明理由.
继续旋转至如图③位置时,(1)中的结论还成立吗?请说明理由.
(3)在图③中,连接BO,AD,探索BO与AD之间有怎样的位置关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com