
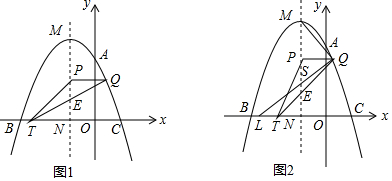
分析 (1)利用待定系数法求二次函数的解析式,并配方求其顶点M的坐标;
(2)根据坐标求出PE的长,证明△TNE∽△QPE,得$\frac{TN}{PQ}=\frac{EN}{PE}$,求出TN的长,代入面积公式可求出S与t之间的函数关系式;
(3)作辅助线,构建直角三角形,利用∠QLD和∠QMP的正切列式,代入可得LD的长,由(2)得TN的长,计算LN•TN可得(t+1)2,则PQ2=TN×LN.
解答 解:(1)把A(0,3)、B(-3,0)、C(1,0)代入抛物线y=ax2+bx+c得:
$\left\{\begin{array}{l}{c=3}\\{9a-3b+c=0}\\{a+b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=-2}\\{c=3}\end{array}\right.$,
∴抛物线y=-x2-2x+3=-(x+1)2+4,
∴顶点M(-1,4);
(2)如图1,由题意得:Q(t,-t2-2t+3),
∵M(-1,4),A(0,3),
∴MN=4,OA=3,
∴ME=OA=3,
∵NE=4-3=1,
∴PE=PN-NE=-t2-2t+3-1=-t2-2t+2,
∵PQ=t+1,
∵PQ⊥MN,TN⊥MN,
∴PQ∥TN,
∴△TNE∽△QPE,
∴$\frac{TN}{PQ}=\frac{EN}{PE}$,
∴$\frac{TN}{t+1}$=$\frac{1}{-{t}^{2}-2t+2}$,
∴TN=$\frac{t+1}{-{t}^{2}-2t+2}$,
∴S=$\frac{1}{2}$PE•TN=$\frac{1}{2}$(-t2-2t+2)$•\frac{t+1}{-{t}^{2}-2t+2}$=$\frac{1}{2}t+\frac{1}{2}$;
(3)如图3,过Q作QD⊥x轴于D,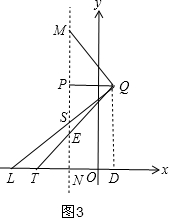
∵MQ⊥QL,
∴∠MQP+∠PQL=90°,
∵∠QMP+∠MQP=90°,
∴∠PQL=∠QMP,
∵PQ∥LT,
∴∠PQL=∠QLD,
∴∠QMP=∠QLD,
∵tan∠QMP=$\frac{PQ}{PM}$,tan∠QLD=$\frac{QD}{LD}$,
∴$\frac{PQ}{PM}=\frac{QD}{LD}$,
∴$\frac{t+1}{4-(-{t}^{2}-2t+3)}$=$\frac{-{t}^{2}-2t+3}{LD}$,
LD=$\frac{({t}^{2}+2t+1)(-{t}^{2}-2t+3)}{t+1}$,
∴LN=LD-ND=$\frac{({t}^{2}+2t+1)(-{t}^{2}-2t+3)}{t+1}$-(t+1)=$\frac{-(t+1)^{2}({t}^{2}+2t-2)}{t+1}$,
∴LN•TN=$\frac{-(t+1)^{2}({t}^{2}+2t-2)}{t+1}$•$\frac{t+1}{-{t}^{2}-2t+2}$=(t+1)2=PQ2.
点评 本题是二次函数的综合题,考查了利用待定系数法求二次函数的解析式、利用配方法求顶点坐标、相似三角形的判定和性质及三角函数,根据相似三角形的性质和同角的三角函数列比例式可求得结论,另外本题的计算量大,容易出错.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
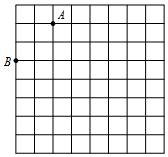 如图是规格为8×8的正方形网格(小正方形的边长为1,小正方形的顶点叫格点),所给网格中按下列要求操作:
如图是规格为8×8的正方形网格(小正方形的边长为1,小正方形的顶点叫格点),所给网格中按下列要求操作:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
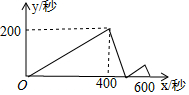 甲、乙两人在同一直线道路上同起点、同方向、同时出发,分别以不同的速度匀速跑步1500米,当甲超出乙200米时,甲停下来等候乙,甲、乙会合后,两人分别以原来的速度继续跑向终点,先到终点的人在终点休息,在跑步的整个过程中,甲、乙两人的距离y(米)与乙出发的时间x(秒)之间的关系如图所示,则甲到终点时,乙跑了1450 米.
甲、乙两人在同一直线道路上同起点、同方向、同时出发,分别以不同的速度匀速跑步1500米,当甲超出乙200米时,甲停下来等候乙,甲、乙会合后,两人分别以原来的速度继续跑向终点,先到终点的人在终点休息,在跑步的整个过程中,甲、乙两人的距离y(米)与乙出发的时间x(秒)之间的关系如图所示,则甲到终点时,乙跑了1450 米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com