
 S△ABC时,求AD的长,并判断此时直线A′C与⊙E的位置关系。
S△ABC时,求AD的长,并判断此时直线A′C与⊙E的位置关系。
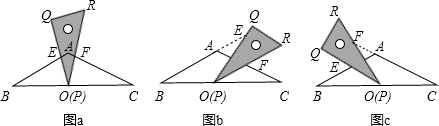
| 解:(1)当A′B′边经过点B时,α=60°; (2)猜想:如图2,点D在AB边上时,m=2; 证明:当  时,点D在AB边上(如图2), 时,点D在AB边上(如图2),∵ DE∥A′B′, ∴  , ,由旋转性质可知,CA=CA′,CB=CB′,∠ACD=∠BCE, ∴  , ,∴△CAD∽△CBE, ∴∠A =∠CBE=30°, ∵ 点D在AB边上,∠CBD=60°, ∴  , ,即m=2; (3)在Rt△ABC中,∠ACB=90°,∠A=30°,BC=1, ∴AB=2, 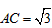 , ,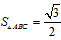 由△CAD∽△CBE 得,  ∵AD=x, ∴  , , 当点D在AB边上时,AD=x,  ,∠DBE=90°, ,∠DBE=90°,此时,  , ,当S= 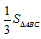 时, 时, , ,整理,得  , ,解得  ,即AD=1, ,即AD=1,此时D为AB中点,故∠DCB=60°,∠BCE=30°=∠CBE, ∴EC=EB, ∵  , ,点E在CB′边上, ∴圆心E到A′C的距离EC等于⊙E的半径EB, ∴直线A′C与⊙E相切。 |
  |


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
 14、把两个一样大的含30°角的直角三角板按如图的方式拼在一起,其中AC平分∠BAF,AD平分∠EAF,请写出所有的等腰三角形:
14、把两个一样大的含30°角的直角三角板按如图的方式拼在一起,其中AC平分∠BAF,AD平分∠EAF,请写出所有的等腰三角形:查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
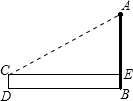 如图,有一位同学用一个含30°角的直角三角板估测学校的旗杆AB的高度,他将30°角的直角边水平放在1.3米高的支架CD上,三角板的斜边与旗杆的顶点在同一直线上,他又量得D、B的距离为15米,则旗杆AB的高度为( )(
如图,有一位同学用一个含30°角的直角三角板估测学校的旗杆AB的高度,他将30°角的直角边水平放在1.3米高的支架CD上,三角板的斜边与旗杆的顶点在同一直线上,他又量得D、B的距离为15米,则旗杆AB的高度为( )(| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com