
【题目】如图,△ABC 和△BDE 都是等边三角形,A、B、D 三点共线.下列结论:①AB=CD;②BF=BG;③HB 平分∠AHD;④∠AHC=60°,⑤△BFG 是等边三角形.其中正确的有____________(只填序号).

【答案】②③④⑤
【解析】
由题中条件可得△ABE≌△CBD,得出对应边、对应角相等,进而得出△BGD≌△BFE,△ABF≌△CGB,再由边角关系即可求解题中结论是否正确,进而可得出结论.
∴AB=BC,BD=BE,∠ABC=∠DBE=60°,
∴∠ABE=∠CBD,
在△ABE和△CBD中,
 ,
,
∴△ABE≌△CBD(SAS),
∴AE=CD,∠BDC=∠AEB,
又∵∠DBG=∠FBE=60°,
∴在△BGD和△BFE中,
 ,
,
∴△BGD≌△BFE(ASA),
∴BG=BF,∠BFG=∠BGF=60°,
∴△BFG是等边三角形,
∴FG∥AD,
在△ABF和△CGB中,
 ,
,
∴△ABF≌△CGB(SAS),
∴∠BAF=∠BCG,
∴∠CAF+∠ACB+∠BCD=∠CAF+∠ACB+∠BAF=60°+60°=120°,
∴∠AHC=60°,
∴②③④⑤都正确.
故答案为:②③④⑤.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】直线 AB∥CD,直线 a 分别交 AB、CD 于点 E、F,点 M 在线段 EF 上,点 P 是 直线 CD 上的一个动点(点 P 不与点 F 重合).
(1)如图 1,当点 P 在射线 FC 上移动时,∠FMP+∠FPM 与∠AEF 有什么数量关系? 请说明理由;
(2)如图 2,当点 P 在射线 FD 上移动时,∠FMP+∠FPM 与∠AEF 有什么数量关系? 请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直角三角板![]() 和直角三角板
和直角三角板![]() ,
,![]() ,
,![]() ,
,
![]() .
.
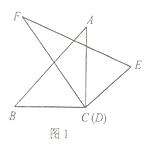
(1)如图1,将顶点![]() 和顶点
和顶点![]() 重合,保持三角板
重合,保持三角板![]() 不动,将三角板
不动,将三角板![]() 绕点
绕点![]() 旋转.当
旋转.当![]() 平分
平分![]() 时,求
时,求![]() 的度数;
的度数;
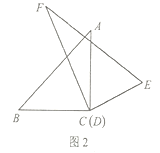
(2)在(1)的条件下,继续旋转三角板![]() ,猜想
,猜想![]() 与
与![]() 有怎样的数量关系?并利用图2所给的情形说明理由;
有怎样的数量关系?并利用图2所给的情形说明理由;
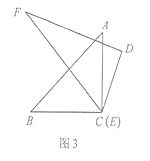
(3)如图3,将顶点![]() 和顶点
和顶点![]() 重合,保持三角板
重合,保持三角板![]() 不动,将三角板
不动,将三角板![]() 绕点
绕点![]() 旋转.当
旋转.当![]() 落在
落在![]() 内部时,直接写出
内部时,直接写出![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
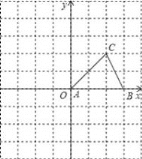
【题目】如图,△ABC的顶点A在原点,B、C坐标分别为B(3,0),C(2,2),将△ABC向左平移1个单位后再向下平移2单位,可得到△A′B′C′.
(1)请画出平移后的△A′B′C′的图形;
(2)写出△A′B′C′各个顶点的坐标;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定,中小学生每天在校体育活动时间不低于1小时,为了解这项政策的落实情况,有关部门就“你某天在校体育活动时间是多少”的问题,在某校随机抽查了部分学生,再根据活动时间t(小时)进行分组(A组:t<0.5,B组:0.5≤t<1,C组:1≤t<1.5,D组:t≥1.5),绘制成如下两幅不完整统计图,请根据图中信息回答问题:
(1)此次抽查的学生数为 人;
(2)补全条形统计图;
(3)从抽查的学生中随机询问一名学生,该生当天在校体育活动时间低于1小时的概率是 ;
(4)若当天在校学生数为1200人,请估计在当天达到国家规定体育活动时间的学生有 人.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.

(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com