
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() 有两个实数根
有两个实数根![]() .
.
(1)求实数![]() 的取值范围;
的取值范围;
(2)若方程的两实数根![]() 满足
满足![]() ,求
,求![]() 的值。
的值。
【答案】(1)k≤![]() ;(2)k=-3.
;(2)k=-3.
【解析】
(1) 把方程化为一般形式,根据方程有两个实数根可以得到△≥0,从而求得k的取值范围;(2)利用根与系数的关系可得x1+x2=2k-2,x1x2=k2,将两根之和和两根之积代入![]() ,即可求k的值.
,即可求k的值.
x2-2kx+k2+2=2(1-x),
整理得x2-(2k-2)x+k2=0.
(1)∵方程有两个实数根x1,x2.
∴△=(2k-2)2-4k2≥0,
解得k≤![]() ;
;
(2)由根与系数关系知:
x1+x2=2k-2,x1x2=k2,
又|x1+x2|=x1x2-1,代入得,
|2k-2|=k2-1,
∵k≤![]() ,
,
∴2k-2<0,
∴|2k-2|=k2-1可化简为:k2+2k-3=0.
解得k=1(不合题意,舍去)或k=-3,
∴k=-3.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
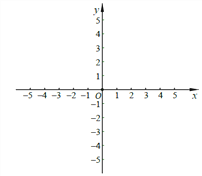
【题目】已知平而直角坐标系xOy(如图),二次函数y=ax2+bx+4的图像经过A(-2,0)、
B(4,0)两点,与y轴交于点C点.
(1)求这个二次函数的解析式;
(2)如果点E在线段OC上,且∠CBE=∠ACO,求点E的坐标;
(3)点M在y轴上,且位于点C上方,点N在直线BC上,点P为上述二次函数图像的对称轴上的点,如果以C、M、N、P为顶点的四边形是菱形,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
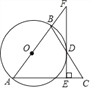
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC交于点D,DE⊥AC,垂足为E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)若∠C=60°,AC=12,求![]() 的长.
的长.
(3)若tanC=2,AE=8,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC.

(1)试用直尺和圆规在AC上找一点D,使AD=BD(不写作法,但需保留作图痕迹).
(2)在(1)中,连接BD,若BD=BC,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】倡导健康生活,推进全民健身,某社区要购进A,B两种型号的健身器材若干套,A,B两种型号健身器材的购买单价分别为每套310元,460元,且每种型号健身器材必须整套购买.
(1)若购买A,B两种型号的健身器材共50套,且恰好支出20000元,求A,B两种型号健身器材各购买多少套?
(2)若购买A,B两种型号的健身器材共50套,且支出不超过18000元,求A种型号健身器材至少要购买多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租车驾驶员从公司出发,在南北向的人民路上连续接送5批客人,行驶路程记录如下(规定向南为正,向北为负,单位:![]() ):
):
第1批 | 第2批 | 第3批 | 第4批 | 第5批 |
|
|
|
|
|
(1)接送完第5批客人时,该驾驶员在公司什么方向,距离公司多远?
(2)若该出租车的收费标准为:行驶路程不超过![]() ,收费10元;超过
,收费10元;超过![]() ,对超过部分另加收每千米1.8元.当送完第5批客人时,该驾驶员共收到车费多少元?
,对超过部分另加收每千米1.8元.当送完第5批客人时,该驾驶员共收到车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
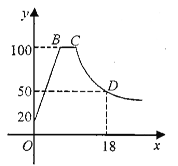
【题目】喝绿茶前需要烧水和泡茶两个工序,即需要将电热水壶中的水烧到100℃,然后停止烧水,等水温降低到适合的温度时再泡茶,烧水时水温y(℃)与时间x(min)成一次函数关系;停止加热过了1分钟后,水壶中水的温度 y(℃)与时间x(min)近似于反比例函数关系(如图).已知水壶中水的初始温度是20℃,降温过程中水温不低于20℃.
(1)分别求出图中所对应的函数关系式,并且写出自变量x的取值范围;
(2)从水壶中的水烧开(100℃)降到80℃就可以进行泡制绿茶,问从水烧开到泡茶需要等待多长时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com