
分析 (1)根据加减消元法可以解答此方程组;
(2)根据分式的除法和减法可以解答本题.
解答 解:(1)$\left\{\begin{array}{l}{x+2y=4}&{①}\\{2x-3y=1}&{②}\end{array}\right.$
①×2-②,得
y=1,
将y=1代入①,得
x=2,
故原方程组的解是$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$;
(2)$\frac{x-3}{x-2}$÷(x+2-$\frac{5}{x-2}$)
=$\frac{x-3}{x-2}÷\frac{(x+2)(x-2)-5}{x-2}$
=$\frac{x-3}{x-2}•\frac{x-2}{(x+3)(x-3)}$
=$\frac{1}{x+3}$.
点评 本题考查分式的混合运算、解二元一次方程组,解答本题的关键是明确它们各自的计算方法.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
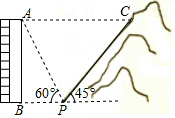 图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时,PC=30m,点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内.
图,一居民楼底部B与山脚P位于同一水平线上,小李在P处测得居民楼顶A的仰角为60°,然后他从P处沿坡角为45°的山坡向上走到C处,这时,PC=30m,点C与点A恰好在同一水平线上,点A、B、P、C在同一平面内.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
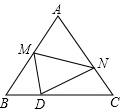 如图,等边△ABC的边长为10,点M是边AB上一动点,将等边△ABC沿过点M的直线折叠,该直线与直线AC交于点N,使点A落在直线BC上的点D处,且BD:DC=1:4,折痕为MN,则AN的长为7或$\frac{65}{3}$.
如图,等边△ABC的边长为10,点M是边AB上一动点,将等边△ABC沿过点M的直线折叠,该直线与直线AC交于点N,使点A落在直线BC上的点D处,且BD:DC=1:4,折痕为MN,则AN的长为7或$\frac{65}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
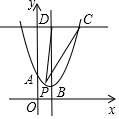 如图,在平面直角坐标系中,点A在y轴上,点A、B($\frac{3}{2}$,m)、C(3,n)均在抛物线y=(x-1)2+1上,点D在抛物线的对称轴上,CD∥x轴.若点P为抛物线上A、B两点间任意一点(包括点A、B),则△PCD面积S的取值范围是3≤S≤$\frac{15}{4}$.
如图,在平面直角坐标系中,点A在y轴上,点A、B($\frac{3}{2}$,m)、C(3,n)均在抛物线y=(x-1)2+1上,点D在抛物线的对称轴上,CD∥x轴.若点P为抛物线上A、B两点间任意一点(包括点A、B),则△PCD面积S的取值范围是3≤S≤$\frac{15}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
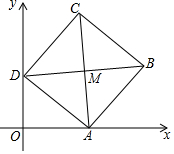 在平面直角坐标系中,正方形ABCD的顶点A,D分别在x轴、y轴正半轴上,AC,BD交于点M,若OA=8,OD=6,则点M的坐标为(7,7).
在平面直角坐标系中,正方形ABCD的顶点A,D分别在x轴、y轴正半轴上,AC,BD交于点M,若OA=8,OD=6,则点M的坐标为(7,7).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:在平面直角坐标系中,直线AB与x轴、y轴分别交于B、A两点,若OA、OB的长分别是方程若x2-7mx+48=0的两根且OB>OA,AB=10.AC平分∠BAO交x轴于点C.
如图:在平面直角坐标系中,直线AB与x轴、y轴分别交于B、A两点,若OA、OB的长分别是方程若x2-7mx+48=0的两根且OB>OA,AB=10.AC平分∠BAO交x轴于点C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com