
 阅读材料:
阅读材料:分析 (1)先把原式化为$\sqrt{(x-1)^{2}+{1}^{2}}$+$\sqrt{(x-2)^{2}+{3}^{2}}$的形式,再根据题中所给的例子即可得出结论;
(2)先把原式化为$\sqrt{{(x-0)}^{2}+{6}^{2}}$+$\sqrt{(x-6)^{2}+{2}^{2}}$的形式,故得出所求代数式的值可以看成平面直角坐标系中点P(x,0)与点A(0,6)、点B(6,2)的距离之和,再根据在坐标系内描出各点,利用勾股定理得出结论即可.
解答 解:(1)∵原式化为$\sqrt{(x-1)^{2}+{1}^{2}}$+$\sqrt{(x-2)^{2}+{3}^{2}}$的形式,
∴代数式$\sqrt{{{(x-1)}^2}+1}+\sqrt{{{(x-2)}^2}+9}$的值可以看成平面直角坐标系中点P(x,0)与点A(1,1)、点B (2,3)或(2,-3)的距离之和,
故答案为(2,3),(2,-3);
(2)∵原式$\sqrt{(x-0)^{2}+{6}^{2}}$+$\sqrt{(x-6)^{2}+{2}^{2}}$的化为的形式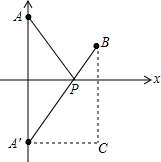 ,
,
∴所求代数式的值可以看成平面直角坐标系中点P(x,0)与点A(0,6)、点B(6,2)的距离之和,
如图所示:设点A关于x轴的对称点为A′,则PA=PA′,
∴PA+PB的最小值,只需求PA′+PB的最小值,而点A′、B间的直线段距离最短,
∴PA′+PB的最小值为线段A′B的长度,
∵A(0,6),B(6,2)
∴A′(0,-6),A′C=6,BC=8,
∴A′B=$\sqrt{A′{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
故答案为:10.
点评 本题考查的是轴对称-最短路线问题,解答此题的关键是根据题中所给给的材料画出图形,再利用数形结合求解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点O的四边形ABCD内一点,OA=OB=OC,AD⊥CD,∠ABC=60°,则∠DAO+∠DCO的大小为( )
如图,点O的四边形ABCD内一点,OA=OB=OC,AD⊥CD,∠ABC=60°,则∠DAO+∠DCO的大小为( )| A. | 100° | B. | 120° | C. | 130° | D. | 150° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 为了测量树的高度,小亮把镜子放在离树(AB)8.1m的点E处,然后观测沿着直线BE后退到点D,这时他恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.7m,小亮的目高CD=1.52m,则树高AB约是4.6m.(精确到0.1m)
为了测量树的高度,小亮把镜子放在离树(AB)8.1m的点E处,然后观测沿着直线BE后退到点D,这时他恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.7m,小亮的目高CD=1.52m,则树高AB约是4.6m.(精确到0.1m)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
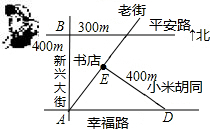 如图,平安路与幸福路是两条平行的道路,且与新兴大街垂直,老街与小米胡同垂直,书店位于老街与小米胡同的交口处,如果小强同学站在平安路与新兴大街的交叉路口,准备去书店,按图中的街道行走,最近的路程为500m.
如图,平安路与幸福路是两条平行的道路,且与新兴大街垂直,老街与小米胡同垂直,书店位于老街与小米胡同的交口处,如果小强同学站在平安路与新兴大街的交叉路口,准备去书店,按图中的街道行走,最近的路程为500m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com