
【题目】已知关于x的一元二次方程x2+ax+nb=0(1≤n≤3,n为整数),其中a是从2、4、6三个数中任取的一个数,b是从1、3、5三个数中任取的一个数,定义“方程有实数根”为事件An(n=1,2,3),当An的概率最小时,n的所有可能值为_____.
【答案】2或3
【解析】
算出相应的概率,判断n的值即可.
(1)当n=1时,△=a2-4b,
①a=2,b=1,△=a2-4b=4-4=0,有实根,
②a=2,b=3,△=a2-4b=4-12=-8<0,无实根,
③a=2,b=5,△=a2-4b=4-20=-16<0,无实根,
④a=4,b=1,△=a2-4b=16-4=12>0,有实根,
⑤a=4,b=3,△=a2-4b=16-12=4>0,有实根,
⑥a=4,b=5,△=a2-4b=16-20=-4<0,无实根,
⑦a=6,b=1,△=a2-4b=36-4=32>0,有实根,
⑧a=6,b=3,△=a2-4b=36-12=24>0,有实根,
⑨a=6,b=5,△=a2-4b=36-20=16>0,有实根.
P(An)=![]() .
.
(2)当n=2时,△=a2-8b,
①a=2,b=1,△=a2-8b=4-8=-4<0,无实根,
②a=2,b=3,△=a2-8b=4-24=-20<0,无实根,
③a=2,b=5,△=a2-8b=4-40=-36<0,无实根,
④a=4,b=1,△=a2-8b=16-8=8>0,有实根,
⑤a=4,b=3,△=a2-8b=16-24=-8<0,无实根,
⑥a=4,b=5,△=a2-8b=16-40=-24<0,无实根,
⑦a=6,b=1,△=a2-8b=36-8=28>0,有实根,
⑧a=6,b=3,△=a2-8b=36-24=12>0,有实根,
⑨a=6,b=5,△=a2-8b=36-40=-4<0,无实根.
P(An)=![]() .
.
(3)当n=3时,△=a2-12b,
①a=2,b=1,△=a2-12b=4-12=-8<0,无实根,
②a=2,b=3,△=a2-12b=4-36=-32<0,无实根,
③a=2,b=5,△=a2-12b=4-60=-56<0,无实根,
④a=4,b=1,△=a2-12b=16-12=4>0,有实根,
⑤a=4,b=3,△=a2-12b=16-36=-20<0,无实根,
⑥a=4,b=5,△=a2-12b=16-60=-44<0,无实根,
⑦a=6,b=1,△=a2-12b=36-12=24>0,有实根,
⑧a=6,b=3,△=a2-12b=36-36=0,有实根,
⑨a=6,b=5,△=a2-12b=36-60=-24<0,无实根.
P(An)=![]() .
.
由以上三种情况可知:An的概率最小时,n的所有可能值为2或3.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
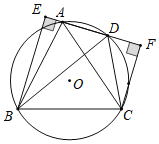
【题目】如图,⊙O是正△ABC的外接圆,点D为圆上一点,连接AD,分别过点B和点C作AD延长线的垂线,垂足分别为点E和点F,连接BD、CD,已知EB=3,FC=2,现在有如下4个结论:①∠CDF=60°;②△EDB∽△FDC;③BC=![]() ;④
;④![]() ,其中正确的结论有( )个
,其中正确的结论有( )个
A. 1
B. 2
C. 3
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
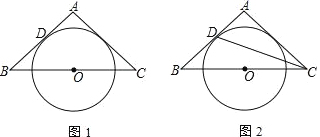
【题目】如图1,△ABC是等腰三角形,O是底边BC中点,腰AB与⊙O相切于点D
(1)求证:AC是⊙O的切线;
(2)如图2,连接CD,若tan∠BCD=![]() ,⊙O的半径为
,⊙O的半径为![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着新能源汽车的发展,某公交公司将用新能源公交车淘汰某一条线路上“冒黑烟”较严重的燃油公交车,计划购买A型和B型新能源公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需300万元;若购买A型公交车2辆,B型公交车1辆,共需270万元,
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该条线路上A型和B型公交车每辆年均载客量分别为80万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1000万元,且确保这10辆公交车在该线路的年均载客量总和不少于900万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11·湖州)(本小题10分)
我市水产养殖专业户王大爷承包了30亩水塘,分别养殖甲鱼和桂鱼,有关成本、销售情况如下表:
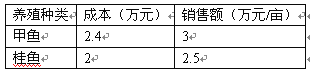
⑴2010年,王大爷养殖甲鱼20亩,桂鱼10亩,求王大爷这一年共收益多少万元?(收益=销售额-成本)
⑵2011年,王大爷继续用这30亩水塘全部养殖甲鱼和桂鱼,计划投入成本不超过70万元。若每亩养殖的成本、销售额与2010年相同,要获得最大收益,他应养殖甲鱼和桂鱼各多少亩?
⑶已知甲鱼每亩需要饲料500㎏,桂鱼每亩需要饲料700㎏,根据⑵中的养殖亩数,为了节约运输成本,实际使用的运输车辆每次装载饲料的总量是原计划每次装载总量的2倍,结果运输养殖所需要全部饲料比原计划减少了2次,求王大爷原定的运输车辆每次可装载饲料多少㎏?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 是矩形纸片,
是矩形纸片,![]() .对折矩形纸片
.对折矩形纸片![]() ,使
,使![]() 与
与![]() 重合,折痕为
重合,折痕为![]() ;展平后再过点
;展平后再过点![]() 折叠矩形纸片,使点
折叠矩形纸片,使点![]() 落在
落在![]() 上的点
上的点![]() ,折痕
,折痕![]() 与
与![]() 相交于点
相交于点![]() ;再次展平,连接
;再次展平,连接![]() ,
,![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .以下结论:①
.以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④△
;④△![]() 是等边三角形; ⑤
是等边三角形; ⑤![]() 为线段
为线段![]() 上一动点,
上一动点,![]() 是
是![]() 的中点,则
的中点,则![]() 的最小值是
的最小值是![]() .其中正确结论的序号是( ).
.其中正确结论的序号是( ).
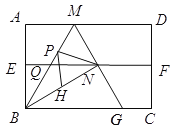
A. ①②④B. ①④⑤C. ①③④D. ①②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
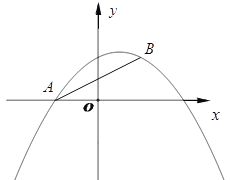
【题目】如图,已知抛物线![]() 经过
经过![]() 、
、![]() 两点,
两点,
(1)求抛物线的解析式;
(2)阅读理解:在同一平面直角坐标系中,直线![]() (
(![]() 、
、![]() 为常数,且
为常数,且![]() ),直线
),直线![]() (
(![]() 、
、![]() 为常数,且
为常数,且![]() ),若
),若![]() ,则
,则![]() .
.
解决问题:①若直线![]() 与直线
与直线![]() 互相垂直,求
互相垂直,求![]() 的值;
的值;
②在抛物线上是否存在点![]() ,使得△PAB是以
,使得△PAB是以![]() 为直角边的直角三角形?若存在,请求出点
为直角边的直角三角形?若存在,请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)点![]() 是抛物线上一动点,且在直线
是抛物线上一动点,且在直线![]() 的上方(不与
的上方(不与![]() 、
、![]() 重合),求点
重合),求点![]() 到直线
到直线![]() 距离的最大值.
距离的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
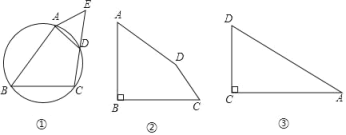
【题目】我们定义:有一组对角相等的四边形叫做“等对角四边形”.
(1)如图①,四边形ABCD内接于⊙O,点E在CD的延长线上,且AE=AD.证明:四边形ABCE是“等对角四边形”.
(2)如图②,在“等对角四边形”ABCD中,∠DAB=∠BCD=53°,∠B=90°,sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() .
.
(3)如图③,在Rt△ACD中,∠ACD=90°,∠DAC=30°,CD=4,若四边形ABCD是“等对角四边形”,且∠B=∠D,则BD的最大值是 .(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
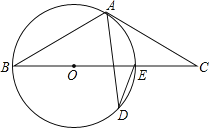
【题目】如图,BE是O的直径,点A和点D是⊙O上的两点,过点A作⊙O的切线交BE延长线于点.
(1)若∠ADE=25°,求∠C的度数;
(2)若AB=AC,CE=2,求⊙O半径的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com