
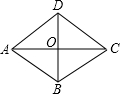
 如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )| A. | 当AB=BC时,平行四边形ABCD是菱形 | |
| B. | 当AC⊥BD时,平行四边形ABCD是菱形 | |
| C. | 当AC=BD时,平行四边形ABCD是正方形 | |
| D. | 当∠ABC=90°时,平行四边形ABCD是矩形 |
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{5}$ | B. | 4$\sqrt{5}$ | C. | 5$\sqrt{2}$ | D. | 2$\sqrt{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{12}$ | B. | $\sqrt{16}$ | C. | $\sqrt{\frac{1}{2}}$ | D. | $\sqrt{{a}^{2}+1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
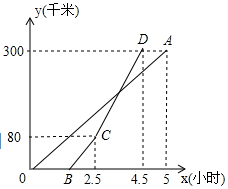 甲乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系,折线BCD表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系.请根据图象解答下列问题:
甲乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系,折线BCD表示轿车离甲地距离y(千米)与时间x(小时)之间的函数关系.请根据图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{8}$÷2=$\sqrt{2}$ | B. | (2$\sqrt{2}$)2=16 | C. | 2×$\sqrt{\frac{3}{2}}$=$\sqrt{3}$ | D. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,BF为⊙O的直径,直线AC交⊙O于A,B两点,点D在⊙O上,BD平分∠OBC,DE⊥AC于点E.
如图,BF为⊙O的直径,直线AC交⊙O于A,B两点,点D在⊙O上,BD平分∠OBC,DE⊥AC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
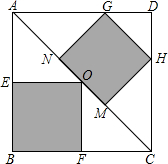 如图,正方形ABCD是一块绿化带,其中阴影部分EOFB、GHMN都是正方形的花圃,其中点N、O、M均在AC上,点G、H、F、E分别在AD、DC、CB、BA上,一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟落在花圃上的概率为( )
如图,正方形ABCD是一块绿化带,其中阴影部分EOFB、GHMN都是正方形的花圃,其中点N、O、M均在AC上,点G、H、F、E分别在AD、DC、CB、BA上,一只自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟落在花圃上的概率为( )| A. | $\frac{17}{32}$ | B. | $\frac{1}{2}$ | C. | $\frac{17}{36}$ | D. | $\frac{17}{38}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com