
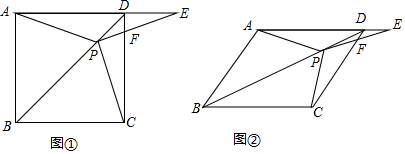
 将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起.
将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起.分析 (1)根据∠DCE和∠ACD的度数,求得∠ACE的度数,再根据∠BCE求得∠ACB的度数;
(2)根据∠BCE和∠ACB的度数,求得∠ACE的度数,再根据∠ACD求得∠DCE的度数;
(3)根据∠ACE=90°-∠DCE以及∠ACB=∠ACE+90°,进行计算即可得出结论;
(4)当CB∥AD时,根据平行线的性质即可解决问题;
解答 解:(1)∵∠DCE=45°,∠ACD=90°
∴∠ACE=45°
∵∠BCE=90°
∴∠ACB=90°+45°=135°
故答案为:135°;
(2)∵∠ACB=140°,∠ECB=90°
∴∠ACE=140°-90°=50°
∴∠DCE=90°-∠ACE=90°-50°=40°;
(3)猜想:∠ACB+∠DCE=180°
理由如下:∵∠ACE=90°-∠DCE
又∵∠ACB=∠ACE+90°
∴∠ACB=90°-∠DCE+90°=180°-∠DCE
即∠ACB+∠DCE=180°;
(4)15°、30°、45°;
理由:当CB∥AD时,∠ACE=30°;
点评 本题主要考查了平行线的性质,以及直角三角形的性质,解题时注意分类讨论思想的运用,分类时注意不能重复,也不能遗漏.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
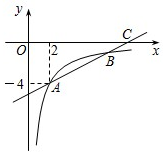 如图,已知一次函数y=kx+b的图象与反比例函数y=$\frac{4-2m}{x}$(x>0)的图象交于点A(2,-4)和点B,与x轴交于点C,且$\frac{BC}{AB}$=$\frac{1}{3}$.
如图,已知一次函数y=kx+b的图象与反比例函数y=$\frac{4-2m}{x}$(x>0)的图象交于点A(2,-4)和点B,与x轴交于点C,且$\frac{BC}{AB}$=$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
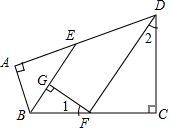 如图,在四边形ABCD中,∠A=∠C=90°,∠ABC,∠ADC的平分线分别与AD,BC相交于E,F两点,FG⊥BE于点G,∠1与∠2之间有怎样的数量关系?为什么?
如图,在四边形ABCD中,∠A=∠C=90°,∠ABC,∠ADC的平分线分别与AD,BC相交于E,F两点,FG⊥BE于点G,∠1与∠2之间有怎样的数量关系?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
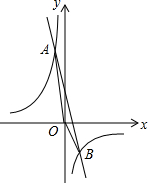 如图,已知反比例函数y=$\frac{{k}_{1}}{x}$与一次函数y=k2x+b的图象交于A(-1,10),B(2,n)两点.
如图,已知反比例函数y=$\frac{{k}_{1}}{x}$与一次函数y=k2x+b的图象交于A(-1,10),B(2,n)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
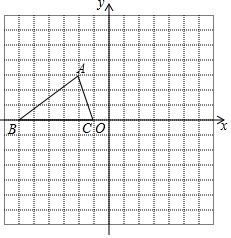 已知,如图所示的正方形网格中,每个网格的单位长度为1,△ABC的顶点均在格点上,根据所给的平面直角坐标系解答下列问题:
已知,如图所示的正方形网格中,每个网格的单位长度为1,△ABC的顶点均在格点上,根据所给的平面直角坐标系解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com